Just About Everything You Need to Know for the ACT Math Section

We can never know what exactly is going to be on the ACT Math section, but each test draws from a similar bank of concepts and terms. This is great news, because it means if you know you tend to struggle on the ACT math section, you can look over this comprehensive list of ACT topics to boost your ACT score.

Some terms and concepts appear on every test, and others appear on every other test or every fourth test. Below is a list of the most common ACT math concepts and how often they tend to appear!

Which Topics are Most Important to Know for the ACT Math Section?

We know this giant list of ACT math concepts seems scary — but don’t worry, we’ll go over each of them in this article. If you see one on the list and you feel like you don’t understand it as well as you could, scroll down for an explanation!

Must Know ACT Math Concepts

These concepts will appear on the ACT Math section. They make up the core material on the exam and students preparing for the test should know these topics first before approaching more

Fractions

Fractions can be expressed in two different ways:

As a ratio of two integers: 2/3. This is the form used when a fraction is equal to a value less than 1 or when when a fraction is larger than 1 but does not simplify to a whole number: 5/2. The latter case is known as an improper fraction, or a fraction where the numerator (top half of the fraction) is greater than the denominator (bottom half of the fraction).
Improper fractions can also be written as a mixture of whole numbers and fractions. For example, 5/2 can also be written as 2 1/2. Since these are a mixture of two different things, these are referred to as mixed numbers.

There are four different ways that fractions can interact: addition, subtraction, multiplication, and division.

For the first two (addition and subtraction), each fraction needs to have the same denominator, known as a common denominator. Once the fractions have the same denominator, they can be added or subtracted as follows:

Add: Add the numerator and keep the denominator (bottom half of the fraction) the same

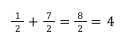
Subtract: Subtract the numerator of the second fraction from the first fraction and keep the denominator the same

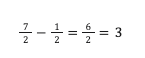
Multiply: To multiply fractions, multiply the numerators of the fractions together, and also multiply the denominators of the fraction together

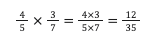
Divide: To divide fractions by each other, it’s easiest to turn division into multiplication. Dividing by a fraction is the same as multiplying by its reciprocal (swap the numerator and the denominator: what was on top will now be on bottom, and vice versa). For example, to divide something by 12, that’s the same as doubling it, or multiplying by 2/1!

Average

The average of a data set is also known as the arithmetic mean.

The mean is equal to the sum of all the data points divided by the number of data points in the set.

How It Will Appear on the Test

Mean-Median Comparison: Many ACT questions about the mean of a data set will ask students to compare the mean and the median: which is larger/smaller or are they the same? Data sets with numbers that are close to one another in value will have similar or identical means and medians. Data sets with more variation (or that are skewed in one direction or another) will have more distance between the mean and median.

Individual Data Point Changes: Questions may also ask: how does increasing or decreasing one of the data points in the set change our mean? What data points would need to be added to get the mean to a particular value?

Calculating Mean from a Table or Graph: Can you calculate the mean of a data set from its histogram? A table of values?

Probability

The probability of an event occurring is equal to the number of successful outcomes (outcomes that fulfill the pre-set criteria) divided by the number of potential outcomes.

For example, to calculate the probability of drawing a red skittle from a bag of skittles, a student will need two pieces of information:

How many red skittles are there in one bag
How many total skittles (regardless of color) are there in one bag

The probability of drawing a red skittles is then equal to: # of red skittles / # of total skittles.

The key for probability questions is whether the question is asking us to add or multiply probabilities together.

Adding Probabilities: Add probabilities when there are multiple different possibilities that will fulfill the probability criteria. So add each discrete probability together to get the total probability.

How does a student know if there are multiple different possibilities that will fulfill the criteria? In the problem above, it is not specified that a particular red skittle is needed (e.g. the heaviest or the largest). Any red skittle will do, so the total probability adds together the individual probability of getting each individual red skittle and that gives the probability of getting a red skittle.

The main key word for an added probability question is: OR. If scenario A or B could be a success, then the probability of being successful is = the probability of A + the probability of B (as long as these two things are not mutually exclusive. In other words, that there is no overlap between these possible outcomes).

Multiplying Probabilities: Multiply probabilities when there are multiple different criteria/steps that each need to be fulfilled in a sequence (or multi-step process). Each step in the process has to be a success, and the probability has to account for the possibility that any given step might have been unsuccessful. This requires multiplication of probabilities rather than addition.

For example, using the skittles setup from above: if a question asks about the probability of drawing two consecutive red skittles, then that will require calculating the probabilities of each individual draw, and then multiplying them together. Another way to imagine multiplying probabilities is as a tree of possible outcomes.

If the odds of drawing a red skittle are ⅔, then on the first draw, there needs to be two branches: the branch where the first draw is successful (which will happen 2 out of 3 times) and the branch where the first draw is unsuccessful (which will happen 1 out of 3 times). Those are the odds of the first draw.

One must then repeat the process for my second draw. Since one may have been successful or unsuccessful on the first draw, the probability has to account for both possibilities when the final probability is calculated. The odds of ending up on one of the final four outcomes branches (for example red, red) = the odds of going down the first branch x the odds of going down the second branch.

It is sometimes possible to get a mixture of multiplied and added probabilities. This occurs in a multi-step process that has multiple possible successful outcomes.

For instance, if a question asked what the possibility of drawing two skittles of the same color (red + red or blue + blue) would be. In that case, the tree still looks the same. But instead of focusing on the odds of one outcome branch, one must instead add up the odds of the two outcome branches that fulfill the goal.

This concept would be written out as this equation: (1/9+ 4/9= 5/9)
It’s worth noting that in the tree above, the probabilities are treated as independent. That is, the odds of one draw do not affect the odds of another draw. However, this is not always going to be the case. It will depend on whether or not I have outcomes that are mutually exclusive.

To understand how mutual exclusivity comes into play, and to look at our above concepts in action, here is question #46 from the December 2020 ACT:

The question wants to know the odds that two car owners drawn from our overall sample will be from the same age bracket. It can be any age bracket, so the question can be restated as: “what are the odds that the first car owner AND the second car owner picked will both be from the 16-25 age bracket OR the 26-45 age bracket OR the 46-60 age bracket?”

The question is asking to find two different car owners. This means that after selecting the first driver, they are no longer going to be in the pool of possibilities that will be selected from: they were selected in the first step, so they cannot be picked in the second step. Therefore, both the numerator and denominator of the probability fraction by 1 (to account for removing one successful possibility from our pool or possibilities). There is one fewer possible successful option and one fewer possible option overall.

So, for this problem, it is necessary to determine what the probability is that one will pick two car owners from each age bracket.

There are 80 16-25 year olds in the sample out of a possible 335 drivers. That means the odds of drawing a 16-25 year old are 80/335. The 2nd draw requires a different person from the same age bracket. So, there are 79 remaining drivers that could be successfully drawn from the 16-25 age bracket. There are also 334 total drivers now remaining. That means the odds of drawing the 2nd person from that age bracket are 79/334.

Both of those steps need to happen to fulfill the question’s criteria. Since step 1 AND step 2 need to be a success, the total probability of drawing two drivers from the 16-25 year old age bracket is (80/335)(79/334).

The process is then repeated for the other two age groups, since each separate age group can fulfill the specified criteria.

There are 155 people in the 26-45 age bracket. The odds of drawing someone on the first go are 155/335 and then 154/335 on the 2nd, since one still cannot draw the same person twice. That makes the odds of succeeding on both the 1st AND 2nd draw (155/335)(154/334).

Similarly, there are 100 people in the 46-60 age bracket. The first and second steps odd are 100/335 and 99/334, and the total probability is their product: (100/335)(99/334).

The odds of picking two drivers from each of the three different age brackets has been calculated. Each of those possibilities represents a successful outcome, and so the answer is the sum of their probabilities:

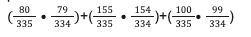
That means that A is the correct answer!

Key Takeaways

Multiple solutions = addition
Multiple steps = multiplication

Mutual Exclusivity = Reduce the numerator and denominator

4. Percents

Percents express what the numerator of a fraction would be if the denominator was 100 (80% = 80/100). 100 is the standard base, and whenever a student is thinking about percentage questions, they must always want to think about that idea of the base.

It is possible to have percentages of numbers other than 100.

75% of 160 = 120. Put another way 75% = 120/160. In this case 160 is the base, and that determines the %.

The most common mistake ACT students make on percentage questions is to accidentally change the base of the percentage fraction, oftentimes without knowing it. ACT percentage questions will always contain wrong answers based off of this mistake.

For example, here is Problem #59 from the June 2020 ACT.

This problem includes two different price markdowns, and so there is a chance to make two different base errors here. Adding together the two discounts 10% + 30% leads to answer E. However, these percentages were discounts off of two different prices (and therefore also two different bases). Trying to add them together is like adding fractions with different denominators: it simply cannot be done.

Instead, a student must use the inverse percentage, so that everything stays in terms of the original price. Saying that something is 20% off of the original price is the same thing as saying it is 80% of the original price.

In the problem above, the sales price of a jacket is 10% off of the original price. This means that the sale price = 90% of the original price, or that the Sale Price = 0.9(Original Price).

The clearance price is 30% off of the sale price. This means that the clearance price = 70% of the sale price, or that Clearance Price = 0.7(Sale Price).

Combining these two equations together, shows that Clearance Price = 0.7(0.9)(Original Price) = 0.63(Original Price).

The clearance price is 63% of the original price, meaning that it is 37% off (100-63) of the original price.

The other wrong answers in this question come from getting caught up with the original percentages given. For example, it is easy to think that since the sales price is 10% off of the original price, then the original price is just 110% of the sales price.

However, that’s flipping the base of the percentage. The store took 10% of the original price, not 10% of the sales price. So adding 10% to the sales price is likely to underestimate the original change. This is why it’s good to simply keep things in terms of the original price Sale Price = 0.9(Original Price).

You are much less likely to make an easy error if you keep things in the units/terms of the original numbers in the problem.

5. Exponents

The main test with exponents is to know when to perform the core three math operations to exponents:

Three Main Exponent Operations

Add:

Exponents are added together when we those exponents share the same base number and that number is multiplied by itself
x² • x⁵ = x^{5 + 2 = 7} = x⁷

Subtract:

Exponents are added together when we those exponents share the same base number and that number is multiplied by itselfThe number in the denominator is subtracted from the number in the numerator.
$$\frac{x^{5}}{x^{2}} = x^{5 – 2\ = \ 3} = x^{3}$$

Multiply

Exponents are multiplied by one another when a base number and its exponent are raised to another power (when an exponent-base pair has an exponent).
(x⁵)³ = x^{5 • 3 = 15} = x¹⁵

There are also three special exponents that students are expected to know. Instead of using operators, these are types of exponents. Students must know the different ways to express these exponents, and how that can then affect the operations listed above:

Special Exponents

Negative Exponents

Negative exponents signify that a number is being taken to the inverse of the given exponent.The exponent expression gets moved from the numerator to the denominator.
$$x^{- 4} = \frac{1}{x^{4}}$$
A key takeaway is that a negative exponent doesn’t lead to negative numbers. The negative here is about inversion, not positive/negative.

Fractional Exponents

Fractional Exponents are another way to express roots.The root that students are generally most familiar with is the square root. Square roots are thought to be the default when the root operator is used. But this could also be written as$$\sqrt[2]{}$$if a student wanted to be clear that it’s a square root (or root 2). This makes then makes it easier to understand the rule that:
$$x^{\frac{1}{2}} = \sqrt[2]{x}$$ The denominator becomes the root power.
$$x^{\frac{2}{3} = \sqrt[3]{x^{2}}}$$ If there is a number other than one in the numerator, that exponent stays with the base number under the radical, even when we switch to the root expression.
It’s important to remember: Fractional exponents do not lead to the base switching from numerator to denominator (as happens with negative exponents)

Zeroed Exponent

Any number taken to the 0 power equals 1.
x⁰= 1 3⁰ = 1 ( − 13)⁰ = 1

6. Linear Equations/Slope

Key Skills

Calculate Slope from Two Points

If given two points on a line, a student should be able to calculate the slope of that line.

The phrase often used to teach this is “rise over run”. Calculate the change in y values and divide it by the change in x values.

$$\frac{y{}_{2} – y_{1}}{x_{2} – x_{1}} = m$$ It’s assumed that the a line moves from left to right when calculating slope, so the y₂value should be the y-value of the right-most point, and the x₂value should be the x-value of the right-most point. The other two values then come from the other point.

Isolate Y (Create y = mx + b)

Sometimes a linear equation will be given in a form other than the classic y = mx + b setup. For these questions, y is treated like any other variable: simply isolate it on the left hand side of the equation.

5X + 5Y = 35 becomes X + Y = 5 (divide whole equation by 5) and then

Y = − X + 5 (−X from both sides)

This is a good reminder that whenever anything shows up on the math section that looks unfamiliar, try out some algebra and see if it can be made to look more familiar. Take the unfamiliar and make it look familiar.

Find Intercepts

The intercepts of a linear equation are where the line hits the x-axis and the y-axis. These are found by setting the opposing variable to zero: equations hit the y-axis/y-intercept when x = 0, equations hit the x-axis/x-intercept when y=0.

For the y-intercept, it’ll be as simple as plugging in 0 for x and then seeing what the output of the equation is. Finding the x-intercept generally requires a little more algebra, as a student works to isolate x.

Key Information for Linear Equations

Perpendicular Slope

When two lines are perpendicular, their slopes are negative reciprocals of each other. That means we can take either slope and find the opposing slope by switching its sign and inverting it between the numerator/denominator.

If there are two lines, m and n, and line m has a linear equation y = 4x + 6, and line n is perpendicular to line m, then it must have a slope of: $$- \frac{1}{4}$$.

“Real Solutions”

“Real solution” questions about linear equations will generally start with two linear equations. What matters for these questions are the slopes and intercepts of the given pair of equations. Based on the number of solutions, the following things will be true about the slopes and intercepts of the two lines:

# of Solutions	Slopes (m)	Intercepts (b)
0	Same	Different
1	Different	Unknown
Infinite	Same	Same

Real solution questions will either have students calculate the number of solutions for a given pair of equations, or it will state a number of solutions and ask students to create an equation that either satisfies this number of solutions (which one CAN be true) or which cannot satisfy that number of solutions (which one CANNOT be true).

Other keywords to look at for are:

Parallel: Parallel lines have no solutions

Intersecting: Intersecting lines have one solution.

Overlapping: Overlapping lines have infinite solutions.

This is a good reminder that another way to think about solutions with linear equations is as “points of intersection”. The solutions to pairs of equations are where those lines intersect on the xy-plane.

7. Solving Equations

Basic Skills

Distribute.

Distributing involves applying a leading coefficient or sign to all of the terms within a pair of parentheses or other grouping of numbers/variables. For example, when a -5 is put in front of the binomial (x + b), it affects both of those terms, even though when it is written out ( − 5(x+b)) the coefficient is located next to the x variable and is separated from the b constant.

This means that when a student “distributes” − 5(x+b) = − 5x − b. It’s important to note that not only the number is distributed, but also the sign. If both the sign on the coefficient and the sign in between the binomial terms are positive, then no signs will change on the terms. If the signs of the coefficient and between the binomial terms are either different or both negative, then a sign change will occur. As soon as a student sees a negative sign or a minus in between binomial terms, they should double check that they’ve distributed the signs correctly.

Combine like terms.

If there are two or more similar terms on the same side of an equation, those terms can be combined. “Like” or “similar” terms means terms with the same exponent and the same variable. This is why a student can combine 3x + 5x but not 3x + 5x².

For example, if an equation looks like: 3x + 17 + 2x − 5= 3x. On the left side of the equation there are two constant terms (terms that are just whole numbers) and two x terms (same variable and same exponent): these pairs can each be combined to simplify the equation.

This is how 3x + 17 + 2x − 5= 3x becomes 5x + 12 = 3x

Special Skills

Creating Equations from Word Problems

Some ACT word problems are much easier to solve with equations, even though the initial question might not provide an equation. Here is an example from the July 2020 ACT

Clearly there are two things that the question wants students to keep track of: time and distance. The key information given by the equation are the two speeds, the directions (due west/east, meaning the drivers are moving horizontally), and the total distance traveled by the two drivers.

In this case, to make the math easier, it’s important to recognize that even though the question asks about the intersection of two different journeys, it’s not necessary to create two different equations. The two drivers will pass each other when they’ve driven a total of 240 miles between them.

The equation that can be created is: 240 = 57x + 68x or (after combining like terms)

240 = 135x. This is because the drivers cover 135 miles (combined) each hour.

$$x\ = \ \frac{240}{125} = 1.92$$ This is the number of hours it will take for the two drivers to pass each other/drive the 240 miles.

Since the question wants a time in minutes, the hours need to be converted: $$1.92\ hours\ \bullet \frac{60\ minutes}{\text{hour}} = 115.2$$ One hour and 55 minutes after the initial departure time = 3:55pm. The answer is D.

8. Picking Numbers

Some questions on the ACT can be made easier by plugging in real numbers in place of variables. Picking numbers can give a student a more intuitive understanding of the problem, instead of keeping things very theoretical.

When choosing numbers for a problem, it can be helpful to try and identify: what is the core mathematical concept the problem is trying to touch on?

For example, let’s look at Problem #41 from the December 2020 ACT.

This problem can be thought about conceptually (meaning leaving the variables in rather than testing actual numbers), but that can be hard to understand sometimes. To make it easier, a student can test out some values and see if they can figure out which statement is true for all values of x. Looking at the possible answers to the question, it is easy to notice that there are four different answers that involve the absolute value.

Since absolute value equations change negatives to positive, it is likely worthwhile to choose a negative number to test. For example, a student can pick the number -2. Once they’ve got the test number, they can start testing to see if each answer is true for the test value (if it’s false for the test value, then it is not true for all values like the question stipulates.)

It’s important to note that test values can prove that a statement is not true, but they cannot necessarily prove that a statement is true.

− x < x − (−2) < − 2 2 < − 2

This statement is not true for all values.

− x < |−x| − (−2) < |−(−2)| 2 < |2| 2 < 2

This statement is not true for all values

x = |x| − 2 = |−2| − 2 = 2

This statement is not true for all values.

|x| = |−x| |−2| = |−(−2)| |−2| = |2| 2 = 2

This statement is true for at least our test value (not necessarily all values)

− |x| = |−x| − |−2| = |−(−2)| − |−2| = |2| − 2 = 2

This statement is not true for all values.

The test value shows that A, B, C, and E are not true for all values, which means that D must be the answer. Again, it’s worth noting that just because D worked at our test value, it didn’t necessarily mean it had to be true for all values. If a student had chosen positive two (2) instead of negative two (-2), some of the statements above would have been true. This is why it was important to choose a negative value, so it was clear how the absolute values affected the outcome.

9. Ratio

Ratios tell the proportional quantity of one thing to another. Ratios are often expressed either with a colon – the ratio of kids to adults is 6:1 (read six to one, meaning there are six kids for each 1 adult) – or like a fraction – the ratio of kids to adults is $$\frac{6}{1}$$.

It’s important to remember that even though ratios can look like fractions, they are not the same thing. Fractions express a part of a whole. Ratios show proportional quantities. Put another way, fractions relate part to whole. Ratios relate whole quantity to whole quantity.

One great example of this is that ratios can be flipped, but fractions cannot. The fraction $$\frac{1}{2}$$is not the same as $$\frac{2}{1}$$. But if a student is looking at a ratio, then the positions of the numbers don’t matter, as long as the labels are kept consistent.

In the kids example, it was given that the ratio of kids to adults is 6:1. This could also be stated as: the ratio of adults to kids is 1:6. As long as both the label and the number are flipped, the meaning stays the same.

This also works if when a ratio is expressed like a fraction:

$$\frac{\text{Kids}}{\text{Adults}} = \frac{6}{1}$$ and $$\frac{\text{Adults}}{\text{Kids}} = \frac{1}{6}$$.

Now, even though ratios express different meanings than fractions, there are certain properties of fractions that can be used on ratios expressed like fractions. For example, if one takes the ratio $$\frac{\text{Kids}}{\text{Adults}} = \frac{6}{1}$$and multiplies both sides by the variable adults, then this leads to the equation Kids = 6 x Adults. So if a student would like to find out the number of kids in a given situation, they can simply multiply the number of adults by 6.

So a student can work with these ratio-fractions as if they’re normal fractions, as long as they keep in mind that they don’t mean the same thing as a normal fraction.

Ratio questions will often ask a student to relate multiple ratios to each either. A student might be given the names of three people, as well as ratios of those individuals’ incomes or heights, for example. They could also be given ratios that ask you to combine information about a larger group, and then information about parts of that larger group. Or they might be given two different versions of the same ratio – simplified and unsimplified – and be asked to calculate one from the other.

For example, here is Question #46 from the April 2021 ACT:

Here the ratios are about advertisement sales. Note that they include the $$\frac{1}{4}$$page number at the beginning just to be confusing. The fact that these advertisements are that size does not affect the answer or how a student should approach the question.

Mary sold twice as many advertisements as Carlos. $$\frac{\text{Mary\ Sales}}{\text{Carlos\ Sales}} = \frac{2}{1}$$

James sold three times as many advertisements as Mary. $$\frac{\text{James\ \ Sales}}{\text{Mary\ \ Sales}} = \frac{3}{1}$$

Since Mary made two sales for every sale that Carlos made, that means that James made 6 sales for every sale that Carlos made. One can find this by rearranging the equations from above to look like: Mary Sales = 2 • Carlos Sales and James Sales = 3 • Mary Sales.

Therefore James Sales = 3 • (2•Carlos Sales) = 6 Carlos Sales

James sold 6 Carlos Sales worth, Mary Sold 2 Carlos Sales worth, and Carlos sold 1 Carlos Sales worth. Therefore, there were 9 Carlos Sales worth of total sales, and Carlos sold 1 out of the 9. So the answer is F.

10. Quadratic skills

There are four crucial skills a student needs to have when it comes to quadratic equations: to factor, foil, zero parentheses, and graph parabolas.

To start, it’s worth remembering what a typical quadratic equation looks like:

ax² + bx + c

There are three terms: a quadratic (squared) term, a linear term, and a constant.

Factor

Quadratics are often expressed in the above format, but the ax² + bx + c form isn’t necessarily super intuitive. Oftentimes, it’s helpful to factor a quadratic equation to make it easier to interpret. Factoring a quadratic means the same thing as factoring a normal number: looking for things that can be multiplied together to get the original number/expression.

To factor the number 27, one can either factor it by expressing it as 27 x 1, or as 9 x 3. The idea is the exact same with quadratics, but now there are both whole numbers and variables to work with.

Quadratic equations will often factor into two binomials (an expression with two terms that are either added or subtracted from one another). Binomials look like: (x + a) or (x−b).

When looking to factor ax² + bx + c, one is first going to look at the aand c terms. That’s because if the quadratic equation factors cleanly, these two numbers will be the product of only two things.

ax²comes from the two x terms multiplied together. c comes from the two constant terms (a and b) multiplied together. Since these two terms are only the product of two numbers, it gives a student the most direct information about what the factors might be.

One usually starts with the c term, since it’s the most basic. C is just the product of two constants. So C is factored like any other integer.

The example quadratic here will be:

x² + 5x + 6

c = 6. The factor pairs of 6 are; 2 and 3; 1 and 6. The binomial factors need to include one of these two pairs.

a = 1. The leading coefficient on the quadratic term is 1, so there are no coefficients in front of the variables in the binomials. The middle term products are also not scaled by anything.

Since the sign on c is positive, the two constants inside the binomials need to have the same sign. Since the middle term b is positive, it’s clear that the constant terms will also be positive.

This equation requires two binomials with no coefficients on the x, which multiply to 6 and add up to 5. Therefore, the factor pair of the constants is 3 and 2.

So factored, the above equation would look like: (x+3)(x+2)

FOIL

FOIL stands for: First, Outside, Inside, and Last. It’s a way to remember how to multiply out two binomials.

The first two terms of each binomial are multiplied together. Then the numbers on the outside of the expression as a whole, followed by the two numbers on the inside of the expression as a whole. Finally, multiply together the last two numbers from each binomial.

These four things are then added together to tell one what the total product of these two binomials is equal to. The First and Last terms normally stand on their own, since they are usually the products of two variables and two constants, respectively. In comparison, the Outside and Inside terms can usually be added or subtracted together, since they will usually both be the product of a variable and a constant.

Check out the explanation in #55 on conjugates below to see why they create quadratic equations with just two terms when FOILed!

Set parenthesis equal to zero

Part of the use of factoring quadratic equations into binomials with variables and constants is that it can make key information about the equation much easier to see. For example, when equations are factored into binomials such as (x−5)(x+3), the x-intercepts of the graph are much easier to find than when the equation is expressed as x² − 2x − 15.

To find the x-intercepts, simply set each parenthetical pair = 0. Another way of thinking of it is to ask: what number would need to be substituted for x to set the parentheses to 0. The answer should always have the opposite sign from the sign in between the two binomial terms. If there is a minus sign, then the answer should be positive. If there is a plus sign, then the answer will be negative.

Graph parabolas

Students should be able to look at a quadratic equation and immediately know what the graph of that equation should look like.

For example, the equation: y = − (x+1)² + 2

The main things to look at when trying to graph a parabola are:

Leading Coefficient

If the leading coefficient is positive then the parabola should be upward facing and the parabola will have a minimum point

If the leading coefficient is negative then the parabola should be downward facing and the parabola will have a maximum point

In the example above, the leading coefficient is -1, meaning that the parabola is downward facing and has a maximum point.

Intercepts

The intercepts show where the parabola will hit its maximum or minimum point.

The x-value of this minimum point is equal to the solution to the parabola’s binomial. In the sample equation above this solution = -1
The y-value of the minimum point is the value of y at the solution point. For the equation above y= − (1−1)² + 2 = 2
Combining these two things shows that the maximum point for the parabola should be at (-1,2)

Equations with Multiple Quadratics

Not all equations will have only one quadratic in them. For example, a problem could ask about the graph of: (x−3)²(x+2)³

There are two key things to look at here:

Exponent: The exponent says what the equation will do at the given intercept.
- If the exponent is linear (raised to the first power), then the function will cross the x-axis at that intercept
- If the exponent is quadratic (raised to the second power), then the function will “bounce” off the x-axis at that intercept
- If the exponent is cubic (raised to the third power), then the function will “slide” at the x-axis (it will cross, but not in a linear fashion. Steeper further from the intercept and shallower close to the intercept)
Intercept: The factors of the equation show how many x-intercepts the graph should have.
- There will be a unique intercept for every unique value of x that could set the equation to 0. This is usually found by looking at the constants in the binomials and seeing if there are any numbers repeated in the parenthesis and which have the same sign. If the sign and constant are repeated, then this does not create an additional intercept.

“Real Solutions” with Quadratic Equations

When a question presents a quadratic equation and asks about “real solutions” or simply “solutions”, there is a two step process to finding the answer the question is looking for.

Step 1: Try to Factor

See if the quadratic equation factors cleanly. If the quadratic equation can be factor into two binomials with whole numbers, then that will always be the quickest and easiest way to find “solutions” to that equation. Because this is the easier way to solve quadratic equations, questions that are designed for this method will often come earlier in the math sections. They also will often be the problems that mention just “solutions” rather than “real solutions”. Non-real solutions tend to show up more during the second step.

Step 2: Look at the Discriminant

$$\frac{- b \pm}{2a}$$ For these questions, it’s necessary to use the quadratic equation. The most important portion of that equation is called “the discriminant”, which refers to the portion of the equation that is underneath the square root: b² − 4ac.

The discriminant determines if there is a negative, positive, or zero number underneath the square root. This then determines how many “real” answers there are to the equation.

A negative number under a square root means that there are only non-real answers (answers that include i (. Zero under the square root means that the equation simplest to just $$\frac{- b}{2a}$$, which since a and b are constants, which will lead to just one answer. And finally a positive under the square root leads to a positive number, which will then be added and subtracted from − b, which then creates two answers.

Discriminant	# of Real Answers
b² = 4ac	1
b² < 4ac	0
b² > 4ac	2

Just like with linear equations, questions about real answers for quadratic equations will either ask a student to find how many real answers there are for a given equation (unlike with linear equations, there is just one quadratic equation, since quadratics can have multiple solutions on their own) or they will ask a student to create an equation that either CAN or CANNOT be true if the equation is to have a given number of real solutions.

11. Area/Perimeter of basic shapes

On the ACT, students may be asked to calculate the areas of certain common shapes, including triangles, rectangles, and circles. The test will provide students with these formulas, but it’s good to be comfortable with using them before the test, so that questions involving these concepts are just about automatic!

Triangle

The area of a triangle is = $$\frac{1}{2}\text{bh}$$ where b is the length of the triangle’s base and h is the height of the triangle. For right triangles the height will be equal to the vertical side coming up from the triangle. For non-right triangles, the height is equal to the distance from the base of the triangle to its opposite corner.

Rectangle

The area of a rectangle is equal to the base times the height.

Circle

The area of a circle is = πr²where r = radius of the circle.

With circles, it’s worth noting that some questions might ask students to use a portion of the area of a circle. This means students just need to use the internal angle measurement of the sector in question to convert the total circle area into the sector area.

12. Negatives

The easiest simple mistake to make on an ACT math section is to make a sign error. Whether it’s addition, subtraction, division, or multiplication, negatives make it easy to switch a sign (or to forget to switch a sign) and lose points on a question that a student would otherwise have gotten right.It’s important for students to be comfortable with how negatives are affected or not affected by the normal math operators: this starts with addition and subtraction.

Negative Operators

Adding negative numbers is just like adding positive numbers. The sum of two negative numbers has the same magnitude as the sum of the same two positive numbers.

a + b = c − a + (−b) = − c

The notation used here is worth paying attention to. Since − b is technically being “added” to − a in the second equation, it has to be put in parenthesis, since two operator signs cannot go next to each other. This can be helpful in preventing mistakes, as whenever students see a parenthesis between an operator and a negative number, that’s a great time to slow down and double check work.

Subtract

Subtracting numbers is a bit different than adding numbers, since subtracting a negative number means taking away something less than zero, which actually translates to adding something. The phrase that many people are familiar with is: two negatives make a positive.

− 5 − (−3)= − 5 + 3 = − 2.

Multiply

Multiplication can either be like addition or subtraction depending on how many negative numbers are being multiplied. If there is an odd number of negative numbers being multiplied by any number of even numbers, then the total product will be negative.

− 5 • 2 • − 4 • 3 • − 2 = − 240

Any two pairs of negative numbers will cancel out their negatives and produce a positive, and any positive numbers added will just keep the product positive. Therefore, if there is an even number of negative numbers being multiplied together with any number of even numbers, then the total product will be positive.

− 2 • 4 • 1 • − 3= 24

Divide

Division is the same as multiplication, but where the pairs of negative numbers have to be in the numerator and denominator to cancel out signs with each other. If both numbers in a fraction are negative, then their signs will divide out and the final product will be positive. If only one of the numbers (in either the numerator or the denominator) is negative, then the final product will be negative.

Negative Tricks

Distribution

The most common way to make a negative sign mistake on any given problem is by not distributing the negative properly when multiple terms are multiplied by the same negative. For example:

− 5(a+4) = − 5a − 20 Since the -5 is right next to the a, it’s easy (on a timed test when a student is rushing) to think that the -5 only distributes to the variable a and to leave the + 4 alone. But since +4 is inside the parentheses, it needs to be multiplied by the -5 when it is distributed.

13. SOHCAHTOA

SOHCAHTOA is a pneumonic device used to remind students of the three trigonometric functions and their equivalents on a right triangle. Problems utilizing SOHCAHTOA will often have students solve for a missing side length on a triangle, or occasionally find a formula to express a side length (where there may only be variables or a mixture of numbers and variables, but where a final number cannot be solved for).

One tip for remembering the letters themselves is that each of the side labels (adjacent, opposite, and hypotenuse) is used twice. There are two Os, two As, and two Hs. Remember either that Tan doesn’t use hypotenuse or that Sin and Cos do, and the rest of the relationships will fall into order.

It’s also worth remembering that these identities are true for both acute angles of a right triangle. And since the labels of “adjacent” and “opposite” are relative to which side is being used, there is some overlap between these identities.

Sin and Cos Overlap

The Sine of the 1st acute angle of a triangle is equal to the Cos of the other acute angle, and vice versa. In our examples above, sinA = cosB and sinB = cosA.

Word Problems

SOHCAHTOA is most common on problems that look like our image above, where there is a triangle on its own and the problem will look to have students solve for a given angle or side. But SOHCAHTOA can also be used to solve word problems.

The triangle may already be drawn in (like the example below) or the question may simply describe a situation that creates a right triangle. The key thing to remember is that: right triangle + trig functions = SOHCAHTOA.

The example below is from the July 2019 ACT. The problem references the following information provided above the question itself: the maximum altitude during Tour C is 1,000 feet.

The angle 37 is used in all of the answer choices, and so the answer will involve SOHCAHTOA, the 37-degree angle, and the height of 1,000 feet.

The question asks about the length of the hypotenuse of the triangle and the question gives the length of the side opposite the angle. Therefore, this is a situation where SOH ($$sin\ = \ \frac{\text{Opposite}}{\text{Hypotenuse}})$$will be relevant.

$$sin37\ = \ \frac{1,000}{c}$$ A little algebra then leads to: $$c\ = \frac{1,000}{sin37}$$. F is our answer.

Extremely Likely (> 80% chance):

14. Function shifts

Vertical Shifts

Vertical function shifts are highly intuitive. They occur from either a coefficient placed in front of the variable(s) in the function or because of a constant term added to the function equation.

Sample Function: y = 2(x+1)² − 5

Here the function is shifted down by 5 units, and is multiplied by a factor of 2. The directions of these changes are intuitive, as they are the same size and direction as the numbers in the equation.

Horizontal Shifts

Horizontal shifts can be a bit more counterintuitive. For example, in the sample equation above the x variable has a + 1 next to it. Following the same rule as for vertical shifts, it would make sense that the x-intercept would then move one unit in the positive direction on the x-axis (to the right).

However, it’s actually the opposite. (X+1) means a horizontal shift one unit to the left. This is also true for leading coefficients. (2X) does not expand a graph in the horizontal direction, it shrinks it.

15. Average sum trick

The average sum trick simply refers to the idea that if a question gives the average of a data set and the number of data points in that data set, then that also allows a student to calculate the sum of all of the data points in the set.

This is equal to: average • # of data points

This is important to know for questions about adding or subtracting data points.

For example:

5 tests, average is 80. After the 6th test, the average is 82. What was the 6th test score?

Average Sum = 80 • 5 = 400

The new average is going to be equal to: (the old sum + the new number)/the updated # of data points

$$82\ = \ \frac{400\ + \ 6th\ score}{6}$$ (82•6) − 400 = 6th score The 6th score was a 92.

This works the same for subtracting a data point. The only difference is that the denominator is reduced by 1 instead of increased by 1, and the removed test score is subtracted rather than added to the original sum.

16. MPH

Miles per hour is a way to express speed: distance covered over a time interval. Questions using MPH often involve some kind of unit conversion. This can be a conversion of distance units (miles to kilometers) or time units (hours to minutes).

MPH also shows up in word problems very often, where a student might need to create an equation with a variable for “hours” (the variable choice is based off of the units that speed is originally given in or that the student is trying to solve towards).

17. Median

The median is the middle number of a data set when the data set is arranged in numerical order. Unlike the mean, it will always be one of the actual data points in the set itself. The set can be arranged as ascending or descending order: the median will still always be in the middle.

When a student wants to find the middle/median number in a data set, they must take the number of values in a data set (n = 23 for example) and divide it by two.

Median of Odd-Numbered Data Sets

In the example listed above, n= 23/2 = 11.5. Because there is an odd number of values in the data set, dividing this number by two results in a nonwhole number. For an odd-numbered data set, we will take this partial number and round it up, in this example to 12. This tells us that the middle number, in other words, the median, is the 12th number in the data set.

Median of Even-Numbered Data Sets

For even-numbered data sets, there is not one number in the middle of the data set. Instead, there are two middle values, and the median is the average (mean) of those two numbers. This is why if there was a sample of 24 data points (instead of the 23 from above), the same operation from above leads to a whole number: 24/2 = 12. The 12th data point is the first of the two median numbers. To get the 2nd number, round up to the next whole number, which tells us that the 13th data point is the second of the two median numbers. The median is then the average of the 12th and 13th numbers.

Remember, for this trick the product of the equations is not equal to the value of the median itself, but merely its “place in line” in the data set. It says where to look, but not what the median is.

How It Appears on the Test

Median questions are similar to average/mean questions. Students will normally be asked to do one of two things. Either they will be asked to calculate the median of a given data set (displayed through a table or graph) or they will be asked to describe how a change in the data set will or won’t change the median (or what change(s) would need to be made to the data set to lead to a certain change in the median).

18. Radicals

Radicals (also known as “roots”) are the opposite of exponents. The most common radical that students are familiar with is the square root or root-2, which is why the default radical symbol is also the square root symbol: . A square root basically says: to get the number under the square root, what number would need to be multiplied by itself to get that number?

Roots above a square root will have a subscript next to the root to show what “degree” the root is taken to. Again, this is the same as exponents where X³means x cubed. In the same way, $$\sqrt[3]{x}$$ is the cube root of x. The first expression says what happens when x is multiplied by itself 3 times. The second expression asks what would need to be multiplied by itself three times to get x.

Radical Operations

Cancel Out

Because radicals and exponents express opposite operations, they can cancel out with each other under certain circumstances. For example, a square root and an exponent of 2 will cancel out with each other.

= x The same thing is true for any evenly balanced roots and exponents

$$\sqrt[3]{x^{3}} = x$$

Multiplication

Two separate square roots multiplied by each other are equivalent to the square root of the products of those numbers

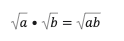
Simplification

The rule above can also be used to help simplify square roots. Instead of combining square roots though, it will involve separating them.

For example, take the square root of 48. This is equal to the product of the roots of its factors: sqrt(48) = sqrt(4⋅12). The square root of 12 is not a whole number, but the square root of 4 is.

Therefore, the expression can be simplified as 2sqrt(12). There are still only whole numbers here, but now if there was a or a 2 in the denominator below , it would be clear that these would cancel out and that the expression could be simplified further.

Whenever a root appears with a whole number underneath it, students should ask themselves: “is there a way to factor this number such that I can simplify the expression?”

This also works when there are variables under the root.

Division

Division with roots is the opposite of multiplication. The ratio of the square roots of two numbers $$\frac{}{}$$ is equal to the square root of the ratio of those two numbers.

Fractional Exponents

As mentioned in the exponents section, roots can be expressed as fractional exponents. If a number has a fractional exponent, then the denominator (bottom half) of that fractional exponent is the root that that number is being taken to.

$$x^{\frac{1}{2}} =$$ This doesn’t affect or change exponents in the denominator. Those remain in the normal exponent spot, even when the fractional exponent is converted to the root form:

$$x^{\frac{3}{2}} =$$

19. System of Equations

System of Equations involves taking a series (usually two) of equations and finding their “solution”, meaning variable values that make all equations in the series true. Another way to think of this is to imagine graphing those equations, and a system of equations problems asking students to find the intersection points between the given equations.

Two Methods for Systems of Equations: Elimination and Substitution

Substitution

The substitution method of system of equations involves isolating a variable in one of the equations, and then plugging in that expression for the variable into the other equation.

For example, if a question gives the following system of equations:

2x + 3y = 2

x − 2y = 8

Then to substitute, a student must choose one equation and one variable to isolate. Isolating the x variable in the bottom equation gives x = 2y + 8. That expression is then substituted in for the x variable in the top equation: 2(2y+8) + 3y = 2. This then leads to 7y= − 14 or y = − 2.

Elimination

Just like with any algebraic equation of coure, one can either work with variables individually or with the equation as a whole. With systems of equations, questions are generally looking for solutions that make both equations true. Since that means the equations must be true statements, the two equations can be multiplied by, divided by, subtracted from, or added to each other, just like any other true statements.

The reason the word “elimination” is used to refer to this is because the most common way to make the two equations in a system of equations interact directly is to subtract one equation from another. Specifically, a student should look to subtract one equation from another such that one of the two variables in those equations is eliminated.

To do this, the variable should have the same coefficient but opposite signs in each equation. This may already be true when the equations are first stated in the problem, or one equation may need to be manipulated to make this work.

In the example above, neither variable has the same coefficient but opposite signs, so a little work would need to be done.

The bottom equation could be multiplied by -2, which would lead to the x variables having same coefficients and opposite signs. A student could also look to eliminate the y variable, but this would require either multiplying one equation by a non-whole number or manipulating both equations. With the ACT, speed is always of the essence, so students should try to choose the quickest/most efficient path!

Therefore, the bottom equation is multiplied by -2: − 2x + 4y = − 16

The two equations are then added together. Technically either side can be added together, but it’s easiest to add the variable sides and constant sides together.

7y = -16 is our sum, or y = − 2. Same answer as our previous method, but just done a little differently.

Deciding Between Substitution and Elimination

Students should do what they’re most comfortable and confident with.

That being said, there are some general guidelines for choosing between these two methods, if a student is comfortable with either approach.

Look at the Numbers in the Equation

First, look at the numbers in the equations. As the following questions:

Are there any shared coefficients and opposite signs in front of the variables?

If yes, that means no work is needed and elimination will be the easiest route.

Are the constants and coefficients factors of each other? Would they divide into each other evenly or cleanly?

If yes, then it could be easy to manipulate the equation and utilize elimination.

If no, then it could be difficult to eliminate numbers easily. substitution may be best.

Look at the Question

What is the question asking for?

Does it want the value of a single variable or of multiple variables or the product/sum of two variables?

If it is asking for a single variable, which cannot be easily reached through elimination, then substitution is often helpful.

If it is asking for the product or sum of multiple variables, especially if that product or sum can be reached through elimination or by leaving an equation intact.

Word Problems

Sometimes problems will involve systems of equations, but the equations will not be directly given by the question. Instead, the problem might be given as a word problem, but where the information presented would clearly lead to the creation of a pair of equations. With these equations there should be two variables, which can be used to calculate two different things: time and distance, for example.

Here is an example question from the April 2021 ACT.

20 = A + B where A and B are the number of courses Susan received an A or B in, respectively

$$3.15\ = \ \frac{4A\ + 3B}{20}$$. Again, we can use either substitution or elimination here.

− 3(20 = A + B) ⇒ − 60 = − 3A − 3B

20 ($$3.15\ = \ \frac{4A\ + 3B}{20}$$) ⇒ 63 = 4A + 3B

3 = A Susan received 3 A’s

One important note: since the question asked for the value of A, B was the variable that the student cancelled out. If A had been cancelled out, then that would have added an extra (and unnecessary) step.

Cancel out or substitute in for the variable that you’re not solving for: this will leave just the variable you’re solving for in the equation.

20. Angle chasing

How Many Degrees in ______ ?

How Many Degrees in a Line

There are 180 Degrees in a Line. This means that if there are two angles across a line, then the sum of those two angles will be 180 degrees. These are known as supplementary angles.

How Many Degrees in Common Shapes

There are a number of common shapes that it is useful to know the number of degrees within.

Triangle: 180 degrees
Square: 360 degrees
Circle: 360 degrees (sometimes also expressed as 2π radians)

How Many Degrees in Any Shape

While normally the common shapes listed above are all that students need to know. Occasionally there are weird shapes in angle problems, and knowing the number of degrees within those shapes may be crucial for answering that question.

Thankfully, there is a simple equation for knowing the number of degrees in any polygon.

Number of Degrees in a Polygon = 180 (# of sides of the polygon−2)

For example, this is why a triangle has 180 degrees:180 (3−1) = 180 • 1 = 180

Vertical/Opposite Angles

Vertical Angles are angles opposite each other at the intersection of two different lines. The lines can have any slope (they do not have to hit at a right angle or anything special). As long as they are straight lines, opposite/vertical angles will be congruent (have the same measure).

In the illustration below, angle a = angle b

Angles at Intersections with Parallel Lines

When a line intersects a pair of parallel lines, there are a number of set relationships between the angles created by those lines. These are useful to know, because they can be massive time savers. You can save a full minute on an angle question just by going beyond just the supplementary angles rule (which can be tedious to work out with many lines or many shapes).

Depending on which pair of angles are being compared, the angles will either be congruent (equal) or supplementary (adding to 180 degrees), as follows:

21. Time

Time Conversions

Be able to convert between different units of time. The most common ones being between hours and minutes and between minutes and seconds.

Time Variables

Some equation questions might have variables that stand in for time, especially as an exponent. The question may then ask for how to maintain the same equation using a different variable for time.

For example, taking the equation T = 100(1.05)^twhere t is the time in hours. If a question wanted this converted to minutes, but without changing the actual equation, then there will need to be compensation for the unit change.

Going from hours to minutes means that the exponent would become larger if there was no compensation. As a result, the new variable will need to be divided by 60 (as this is the number of minutes in an hour).

Therefore, the new equation would look like: $$T = 100(1.05)^{\frac{m}{60}}$$where m is the number of minutes.

The key for keeping equations consistent while changing exponent variables is that if you’re subbing in a bigger variable, then it will need to be divided by something, and if you’re subbing in a smaller variable, then it will need to be multiplied by something.

22. Pythagorean Theorem

This is one of the most fundamental concepts in math, and as a result it is something that will be applicable on every single ACT. The pythagorean theorem applies to right triangles and states that the square of the hypotenuse is equal to the sum of the squares of the other sides.

A question may simply show a triangle directly and ask for either the side lengths or a calculation that requires knowing all of the side lengths (such as perimeter). This may also be usable in a word problem.

Be on the lookout for if a word problem explicitly states that something happens at a 90-degree angle or if there is a perpendicular line or tangent line. These all lead to 90 degree angles and mean that a right triangle may be created, and so the pythagorean theorem is valid.

23. Apply formula

Applying formula problems will provide a student with a particular formula/equation, and will then ask a student to properly plug in numbers into that equation to calculate something. This will often be done in the context of a word problem that describes the real-world application of the equation. For these equations the main tricks are to:

Clearly identify the dependent and independent variables. The independent variables are what is being changed in the equation (in the cause/effect chain, they are the cause). The dependent variables are the outputs of the equation. THey are the result of the change made.

Be sure to remain consistent with units. The original formula might be given in hours, but then the number that has to be plugged in is in minutes. Remember that the original formula is the guide, and that everything should be kept consistent with that guide.

24. Composite function

Composite functions are where one function is put inside of another. This can look intimidating at first, but these problems are quite simple once a student gets the hang of it.

Inside Out

It’s easiest to think of composite functions as a priority list or an order of operations. Work from the inside to the outside.

Here is an example from the June 2020 ACT:

Working from the inside out. g(−1) = (−1)² − 1 = 1 − 1 = 0. Since g(−1) = 0, g(−1) can be replaced with 0, as if it was a variable that we had solved for and could now plug into an equation.

Now the next layer: f(0) = 2(0) + 3 = 3. The answer is 3!

25. Matrices

A matrix is a series of rows and columns used to display numbers. ACT questions about matrices will generally be about performing fundamental math operations such as addition, subtraction, or multiplication between matrices.

Is It Possible?

A key note is that not all matrices can be added, subtracted, or multiplied.

Two matrices can only be added or subtracted if they have the same dimensions
Two matrices can only be multiplied if the number of columns in the first matrix is equal to the number of rows in the second matrix

Adding and Subtracting

Adding and subtracting matrices is quite simple. Since the matrices have to have the same dimensions, each number has a “twin” that shares the same space in the opposite matrix.

Matrix addition means adding each pair of numbers in the same places in their respective matrices. Subtraction means subtracting pairs.

The resulting matrix will have the same dimensions as each of the original matrices.

Multiplying

Multiplying matrices is a bit more complicated. Matrix multiplication is used to find the dot product. This is sometimes the term used on the ACT to imply matrix multiplication.

As stated above, matrices can only be multiplied if the number of columns in the first matrix is equal to the number of rows in the second matrix. The top left number in the dot product is equal to the sum of the numbers in the first row of the first matrix multiplied, in order, by the numbers in the first column of the second matrix.

The next number down in the dot product’s first column is equal to the numbers from the second row of the first matrix multiplied, in order, by the numbers in the first column of the second matrix.

This is then repeated until there are no more rows left in the first matrix. The process is then repeated again for the next column in the second matrix.

The final dot product will have the same number of rows as the first matrix and the same number of columns as the second matrix.

26. Midpoint

Midpoint questions involve working with two ordered (x,y) pairs and finding their midpoint. This is done using the following equation:

$${(x}_{M},y_{M}) = (\frac{{x_{1}}_{} + x_{2}}{2},\frac{{y_{1}}_{} + y_{2}}{2})$$, where (x_M, y_M) is the midpoint and the x and y values on the right side of the equation are from the ordered pairs of that midpoint.

Occasionally these questions might give the midpoint and one of the ordered pairs, in which case a student must use normal algebra on the above equation to find the missing pair. Each variable will need to be dealt with separately for that algebra to work (it cannot be done simultaneously).

Very Likely (> 50% chance):

27. Special Right Triangles

There are certain special triangles that students might be expected to know on the math section of the ACT. Like the formulas for the area of a circle or rectangle, these identities are normally presented to students at the beginning of the test, and so the challenge is knowing how to identify problems where these identities are relevant and how to use them to solve relevant problems.

The most common special triangles are: 45-45-90 and 30-60-90 triangles.

Because these length and angle relationships are set, any time these angles appear or these side lengths appear, they can give us useful information for solving a problem. Problems involving these triangles often utilize words/drawings or the xy-plane. They are also often relevant on problems involving triangles and points of tangency. For example:

Since the square touches both the center and the perimeter of the triangle, a line going from one corner of the square to the other corner will be equal to the radius of the circle. This straight line divides the square perfectly in half, which means that the angles on each side of the line are = 45 degrees. That means that this square can be defined as follows:

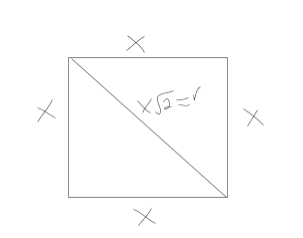
The question gives us the area of the shaded region, which equals 36π − 18. From the image, it’s clear that this is equal to the area of the circle minus the area of the square. In other words:

πr² − s² = 36π − 18 where r is the radius of the circle and s is the side lengths of the square. The triangle above shows that r = x. Plugging this into the formula above gives:

π(x)² − x² = 36π − 18

2x²π − x² = 36π − 18

x²(2π−1) = 18(2π−1)

x² = 18 x= x = 3

x was equal to the side length of the square and the question asks for the perimeter of the square. Therefore, the answer is: 4(3) = 12 and so C is the correct answer.

28. Absolute Value

|x| (absolute value of x) is the magnitude (the non-negative value) of x, regardless of its original sign.

The concept of an absolute value revolves around negative and positive numbers. A positive number doesn’t change when placed in an absolute value, but a negative value does change: it becomes a positive. Therefore, if a problem involves an absolute value, it’s a good idea to pay attention to any negative numbers in the problem (or to use a negative number as a test value like in one of the above practice questions).

29. Multi Step conversion

Multi-step conversions will involve a mixture of ratios and/or equations. Questions will either go from a proportional ratio to an overall total, or they will ask for a conversion of one ratio to another (usually in the form of a unit conversion).

One of the most common versions of this question will involve mph and gas costs in miles/gallon.

For example, a problem might say that a person can drive their car, which gets 50 miles-per-gallon, for a maximum of 1,340 miles. If gas costs $$3.28/gallon, how much would it cost to fill the car’s tank?

Since the cost is based on the number of gallons, the mpg and mileage must be used to calculate the size of the car’s tank. If they can drive a maximum of 1,340 miles getting 50 miles-per-gallon, then that means the car has a tank that holds 26.8 gallons.

Therefore, the cost of filling the tank is: 26.8 * $$3.28 = $$87.90.

30. Remainders

Remainder problems will generally either be: simple or pattern-based reminders.

Simple

Simple remainder questions will provide some kind of division problem, which will leave some remainder. The student will then generally have to find whatever whole number is left over when the nearest factor of the denominator is taken away from our original number.

For example: what is the remainder when 2387 is divided by 38?

$$\frac{2387}{38} = 62.816$$ This means that the nearest factor of 38 to the original number is 38 * 62 = 2356

The remainder is therefore: 2387 − 2356 = 21

Pattern-Based

For pattern-based remainder questions, the question will provide some kind of repeating decimal, and will then ask for a large-numbered digit of that repeating decimal: for example, the 4567th digit after the decimal point. A repeating decimal means that there is an infinite string of digits after the decimal, which repeat in a set pattern.

The repetition often starts next to the decimal, or after the first two digits of the decimal. For example, 1/12 = .08, so the first two numbers after the decimal point are not a part of the repeating pattern.

Key takeaway: not all numbers after the decimal point have to repeat for there to be a pattern.

Just like with patten-based remainder questions, factors are still key. However, instead of being interested in the factors of the denominator in a fraction/ratio, pattern-based remainder questions are more about how many digits repeat in the decimal pattern.

Common Repeating Decimals

Repeating-decimal questions can create or provide any decimal or pattern, but there are some common repeating decimals that might show up. The most common repeating decimals to show up on these questions (or even other questions) are:

1/6 =.1666

1/9 = .111 For any fraction with 9 as the denominator, the repeating decimal is simply equal to the numerator repeating after the decimal point (2/9 = .222)

1/11 = .090909 For any fraction with 11 as the denominator, the repeating decimal is simply equal to the numerator multiplied by 9 (expressed in two digits) after the decimal point (2/11 = .181818)

1/12 = .08333

31. Weird shape area

Some ACT Math area questions will involve shapes that are irregular, meaning that they are not the standard triangle, circle, rectangle, or square. Instead, they might simply be polygons that combine portions of these shapes together.

For weird shaped area problems, break down the large, weird shape into smaller, more familiar shapes. Just like with equations, it’s about making the unfamiliar seem more familiar.

Sample Problem

Here is an example problem from the July 2019 ACT:

There are two different ways to approach this problem. Either, the area of the original rectangle can be calculated, as well as the squares that were removed, and then the two numbers can be subtracted. Or the remaining shape can be broken down into a group of five rectangles, and their areas can be summed up together.

Now, since the answers to the question all involve subtraction, it would make sense that the subtraction method might work best in this case.

The original area of the rectangle was 18 • 8 = 144. The area of each square removed was equal to x². Four of these squares were removed, and so the area of the remaining rectangle is 144 − 4x² or G.

Key Takeaways

With weird shape areas it’s often helpful to remember that weird shapes are made from cutting out familiar shapes from familiar shapes, or by adding familiar shapes to familiar shapes.

Also remember that especially when it comes to shapes made from cutting things out. There are some quick rules to remember about how this affects the areas and perimeters of the shapes.

Area: Just like the question above, remember that the area of the larger shape can still be calculated to find the area of the new shape. It’s just about remembering to take away the areas of the shapes that were cut out.
Perimeter: A slight more fun trick. If the shapes that are cut out from the original shape are rectangles (are made up of only perpendicular lines), then the perimeter of the new shape is the same as the perimeter of the old shape. So in the above example, the original rectangle and the new shape would have the same perimeter.

The perimeter trick is particularly useful for saving time on questions. Perimeter doesn’t change by taking rectangles out of shapes.

32. Periodic function graph

Sine and Cosine graphs appear fairly frequently on the ACT math section. It is less likely that you’ll be asked to calculate specific values on the graphs (though this does happen occasionally).

Instead, it’s much more likely you’ll be asked to:

Look at a graph and identify a possible equation for that graph
Be given an equation and asked to identify an accurate graph of that equation

Either of these types of questions can be quite easy, as long as a student remembers some key facts about the sine and cosine graphs.

Basic Principles

The Sine and Cosine functions are wave functions. They repeat forever making the same pattern. The values for the sine and cosine graphs are the same values that one could find by looking at the unit circle.

Sine and Cosine graphs look almost identical, but they start at slightly different places. The Sine graph starts at the origin (0,0), while the Cosine graph starts at (0,1). Therefore, the two graphs are basically the same, but shifted by $$\frac{\pi}{2}$$in the x-direction from each other.

Amplitude

The Sine and Cosine functions have the same amplitude, which is the distance from the center line (the x-axis for the default graph) to the maximum point of the graph.

The default amplitude of the Sine and Cosine graphs = 1

Period (Frequency)

The period of a repeating graph like sine and cosine refers to how long the graph needs to go along the x-axis until it begins to repeat. The period of the sine and cosine graphs is also the same.

The default period of the Sine and Cosine graphs = 2π

Shifts

The Sine and Cosine graphs are affected by x and y shifts just like any other functions. Y shifts will affect the amplitude of the graphs, while x shifts will affect the frequency.

Shifts are accomplished either through the addition of leading coefficients in front of the variables or by adding constant terms next to the variables.

Y-Shifts

Y-Shifts are more intuitive. When a constant is added to the sine or cosine function, it shifts the graph up or down based on the number and sign of the constant.

If the y constant is positive, the graph shifts up, and if the y constant is negative, the graphs shifts down.

The same is true for coefficients in front of cos(x) or sin(x). Coefficients greater than 1 will stretch the graph up/down, while coefficients smaller than 1 will compress the graph.

X-Shifts

Just like with other functions, X-shifts are a bit more counterintuitive. For example, the graph of sin(x + 1) shifts left instead of to the right. Also, sin(4x) compresses the graph by a factor of 4, rather than expanding it by that amount.

The easiest way to think about this is that by affecting the x value, the amount of work being asked of the x variable is changing. If each x variable is multiplied by 4, then that means that it only takes a number ¼ as big to get the same output, and so everything compresses to account for that.

Similarly, with (x + 1), the number -1 will produce the same output that x = 0 used to create, and so the graph has to shift one unit to the left to account for this.

In summary:

Sine and cosine are repeating wave functions when graphed. They have an amplitude of 1 and a period of 2

Y-constants and coefficients in front of sin/cos will stretch or move the graph proportionally with these added terms

Constants and coefficients inside of the sin and cos with the x variable will stretch or move the graph in the inverse direction of that coefficient/constants sign or magnitude

Sample Problems

This can be one of the trickier concepts at first, but with a little practice these questions can become quick and easy. Here are two sample problems to give some practice:

The question does not identify which of the two graphs is sine or cosine, but since the dotted line graph starts at the origin and the solid line graph starts above the origin, it’s clear the solid line is the cosine graph and the dotted line is the sine graph.

The sine graph has a higher amplitude than the cosine graph, which means that its coefficient must be larger than that of the cosine graph (a₁ > a₂). Since the sin graph has been stretched out, it’s also clear that a₁ > 0. As a result, the answer must be B.

This question is a more direct example of quantitative shifts. The Cosine function normally starts at (0,1), but in this graph that is now (0,3), meaning that the equation has been stretched out by a factor of 3. This eliminates answers F and G.

Looking next at the period, the graph appears to repeat after x = π . This means that the graph has been compressed along the x-axis, which means the x value is multiplied by a coefficient greater than 1. Only K does both things correctly and so this is the answer.

33. Shaded area

Shaded area questions will generally involve one of two things: a geometric shape (or possibly one inside of the other) or an inequality graph.

Geometric Shading Problems

Geometric shading problems will focus on calculating area. Students will be asked to calculate a shaded area from a larger whole area. This will often involve subtracting one area from another.

The most common version of this is to have a square inside of a circle or vice versa. It may also involve a triangle inside a sector of a circle. The question would then ask for the area of the circle sector minus the area of the triangle.

Inequality Graphs

Inequality shading problems will focus on identifying areas on a graph. Students will need to identify which area above or below a line should be shaded, or which portions of a shape should be shaded to satisfy an inequality.

Like with normal inequality problems, the easiest way to approach these questions is to replace the inequality sign with an equal sign. Normal algebra rules then apply for the equation: isolate the y on the left hand side to make it look like the usual y = mx + b form.

Here is an example problem from the June 2017 ACT:

ax + by = c can be rewritten as $$y = \ \frac{- ax}{b} + \frac{c}{b}$$. Remembering that 0 < a < b < c. The slope of the line will be negative, so the line should be downward sloping. This eliminates F. $$\frac{c}{b}$$is positive, so the y-intercept should be positive: this eliminates J and H.

The only difference between G and K is that one has shading below the line, while the other has shading above the line.

Shading above a line means that y should be greater than the other side of the equation
Shading below a line means that y should be less than the other side of the equation

The inequality version of the equation is: $$y \leq \ \frac{- ax}{b} + \frac{c}{b}$$. Y is less than the other side of the equation, meaning that the shading should be below the line.

This means the answer is K.

34. Counting principle

Counting principle questions are similar to probability questions, but instead of probabilities they are asking about possibilities. Often in ways such as: how many different possible combinations are there of several different groups of items or options, such as letters and numbers for a license plate or dice rolls from multiple pairs of dice (possibly with different sets of numbers).

The counting principle simply states that if there are x possible ways to do one thing and y possible ways to do another thing, then there are x • y possible ways of doing both things. So count and then multiply.

This can be thought of in a similar way to multiplying probabilities from above, but where the tree branch of options is more about the possibilities created by each branch rather than what proportion of them is successful. Basically only the denominators calculated for that tree matter, rather than the whole fractions.

Here is an example question from the December 2017 ACT:

Single digits 0 through 9 = 10 possible numbers that can be chosen

Letters of the alphabet = 26 possible numbers that can be chosen.

Single digits must be chosen for each of the first three slots and they can repeat. Therefore, the are 10 ways to fill slot #1, 10 ways to fill slot #2, and 10 ways to fill slot #3 = 10 • 10 • 10 = 1, 000 possibilities. This is how many possible ways the first three slots can be filled.

The last three slots require letters. There are 26 ways to fill each slot, and so there are 26 • 26 • 26 = 17, 576 possibilities. This is how many ways the last three slots can be filled.

How many ways can all 6 slots be filled= first three possibilities x last three possibilities = 1, 000 • 17, 576 = 17, 576, 000. Our answer therefore is K.

35. Logarithms

A logarithm is the inverse of taking something to an exponential power. When something is expressed as log₅125, in a sense it’s asking what exponent would 5 need to be taken to to get 125. This is why log₅125 = 3.That’s why the first core skill of logarithms is to be able to rewrite logs in exponential form.

Rewrite Exponentially

If given log_ax = b, be able to rewrite this formula as a^b= x. This will make any question asking you to solve for a variable in the original equation much more intuitive and easy to answer.

Log Operations

In the same way that exponents have certain rules for fundamental math operators, logarithms have their own rules for adding, subtracting, multiplying, and dividing. Just like with exponents, these rules generally rely on having the same base number.

Add

Log_a(X•Y) = Log_aX + Log_aY The log of any given number is equal to the sum of the logs of its factors. Or read the other way, two logs added together is equivalent to the log of their product

Subtract

$${\text{Log}_{a}(\frac{X}{Y})}_{} = \text{Log}_{a}X\ – \text{Log}_{a}Y$$ The log of any given fraction is equal to the log of the numerator minus the log of the denominator. Or read the other way, one log subtracted from another is equal to the ratio between those two numbers.

Special Skills and Facts

Moving Exponents

Since logs are related to exponents, exponents that are a part of a log can be moved around in a convenient way! Specifically, exponents on numbers inside of the log function can be moved in front of the log and turned into a linear coefficient.

For example log_a x², can be rewritten as 2 log_a x.

Natural Log

A normal logarithm uses the shorthand log, but there are other types of logarithms that are commonly used in math and other fields. THe most common one is the natural log, which is written as ln x. This still follows the same rule as any other log, but instead of being the log of an integer, natural log is log base e, where e is the special number known as

Log Base 10

In the same way that without a specific number on the radical is understood to mean the square root. A log without a specified base is understood to mean log₁₀.

Log 1

Another great example of how log rules relate to exponent rules. Any number taken to the power of 0 = 1. So, Log 1 = 0, no matter what the Log base is.

36. Imaginary numbers

Imaginary numbers refer to irrational numbers that cannot exist in the real word, but which do exist in math. The most common imaginary number to see on the ACT is the imaginary number i, or the square root of -1.

When in Doubt, Try to Square It

The best piece of advice for problems involving i, especially those that involve calculating a real number or simplifying a fraction such that it only contains real numbers is:

See if there is a way to square i. Since it is equal to -1, squaring i can take an imaginary number and make it a real number
When i is part of a binomial in the denominator, it may require using a conjugate to simplify out i. See #55 on this list for a longer explanation of conjugates.

Powers of i

On the ACT, it’s worth knowing not only that i = , but also that there is an easy way to know what i raised to any power is equal to. i goes through a pattern of four different values, depending on what power it is raised to. These values always go in the same order, and as long as a student knows how the pattern starts, they can always figure out the value of i to any exponent.

Any number taken to the 0 power is = 1, and so i⁰ = 1.
i = , and so i¹=

Any square root squared is simply equal to the value underneath the square root, so i² = ()² = − 1

Since i² = − 1 and i¹ = i, then i³ = i¹ • i²= − 1 • i= − i

And finally, i² = − 1 and so i⁴ = i² • i²= − 1 • − 1= 1

And so the pattern of ilooks like: 1, i, − 1, − i.

To figure out the value of i at any given exponent, simply take the exponent and find it’s nearest factor of 4. The conversion chart then looks like:

Remainder After Factor	Value
0	1
1	i
2	− 1
3	− i

The Complex Plane

Occasionally ACT problems involving i will include the concept of the “complex plane”.

This means that the xy plane is replaced with a plane that includes:

real numbers on the x-axis
imaginary numbers such as i on the y-axis.

37. Least Common Multiple (LCM)

The Least Common Multiple refers to the smallest possible number that is evenly divisible by a given pair or set of numbers. For example, the least common multiple of the numbers 2 and 3 is 6.

The easiest trick for finding the least common multiple of any series of numbers is to find the multiples of the largest number in the set, and find the first of those numbers that is evenly divisible by both of the other two numbers.

For the set 4, 10, and 25. Go through the multiples of 25 until one is evenly divisible by both 4 and 10. The first number that satisfies this is 100, so this is the least common multiple of this set of numbers.

38. Scientific notation

Scientific Notation is a way to express very large or very small numbers by the number’s most significant digits combined with an exponential expression of base 10. This notation usually includes a whole number with one or two decimals after it: 2.38. This will then be followed by an exponential expression of: × 10^a , where a is going to either be a positive or negative number, generally with a magnitude greater than 3.

The exponent on the 10 shows if the number is a very large number or a very small number. If the exponent is positive, then the number being expressed is quite large. If the exponent is negative, then the number being expressed is very small.

The magnitude of the exponent then tells you how many places the original digits were moved by to get to the new expression. In other words, how many places were originally between the decimal point and the new currently visible digits of the number.

For example, 6.52 × 10⁸is another way of writing 652,000,000. The scientific notation version is raised to the 8th power because in our original number there were 8 places between the leading 6 and the decimal point. It’s important to note that this would be the same even if the number were 6.2 × 10⁸, but there would be 7 0s instead of 6, as now there is one fewer significant digit before the decimal point.

The inverse is true for when there is a negative exponent instead of a positive one. It’s still the number of places between the original decimal point and the first significant digit, but now it’s to the right of the decimal point instead of the left.

6.52 × 10⁻⁸ is another way of writing .0000000652. The simple conversion is the whole number will move to the right of the decimal point, and then zeroes are inserted. The number of zeros = |Exponent|− 1. In other words since the exponent here is -8, there are 7 zeroes added rather than 9 (8-1 rather than − 8 − 1).

The last thing to note is that with positive scientific notation, sometimes there are two or three digits after the decimal point that “absorb” some of the zeroes places that are being multiplied by. With the negative exponents, there is generally just the single digit whole number to the right of the decimal, and so the number of zeroes will always be equal to that exponent minus one rule.

39. Ellipses

Ellipses are a rare but important shape to know about for the ACT math section. Here are the main properties of an ellipse that students will be expected to know:

Key Skills for Ellipses

What is an Ellipse?

An ellipse is an oval shape. It is similar to a circle, but where one of its axises is stretched. As a result, an ellipse has both a major axis and a minor axis.

The major axis is the axis in between the longer ends of the oval

The minor axis is the axis in between the shorter ends of the oval

Reading and Graphing Ellipse Equations

Since the shape of an ellipse is similar to a circle, the equation is similar too. An ellipse equation will look like this:

$$\frac{(x – 1)^{2}}{9} + \frac{(y + 2)^{2}}{1} = 1$$

Unlike the circle equation, there are now denominators under the squared binomials. This is to differentiate the lengths of the major and minor axes.
The ellipse equation will always be = 1

Like with the circle equation, the constants inside of the binomial indicate where the center of the ellipse is.

(x-1)2 means that the center point lies along the vertical line x=1

(y+2)2means that the center point lies along the horizontal line y= -2

Combining these two things means the center is at (1,-2)

The denominator term is then equal to half the length of the major/minor axis squared.

The denominator under the x term is 9, meaning that the each half of the major axis has a length of 3
The x-axis is the major axis because it has a larger denominator, and therefore its axis is longer
The denominator under the y term is 1, meaning that each half of the minor axis has a length of 1

ACT questions about ellipses may give an ellipse equation and require students to graph it to find a point on the ellipse or the center point of the ellipse. A question could also provide a graph of an ellipse and then provide several equations, from which the student must then select the equation that correctly matches the graph.

40. Vectors

Vectors are a way of expressing magnitude (size) and direction. The magnitude of a vector will often be described using variables, most commonly the variables i and j. The direction of the vector will be indicated by an arrowhead at the end of the vector line.

Vector Skills

There are three main operations students might be asked to perform on vectors: addition, subtraction, and multiplication.

Adding

To add together any two vectors, take each vector and attach it to the endpoint of the vector that it is being added to. This will create a diamond shape. The diamond starts where the two vectors start, and it ends where they meet (after being added on to the other vector).

The sum of the two vectors is then equal to a new vector created by going from one end of the diamond to the other. The direction/arrow of this new vector will move in the same direction as the two added vectors.

Subtracting

Subtracting vectors is similar to addition. However, instead of simply attaching both vectors to their ends of their added pairs, first one of the vectors has to be flipped.

Specifically, the vector that is being subtracted needs to have it’s direction flipped (though it’s magnitude remains the same).

This flipped vector is then added to the other, original vector using the same diamond pattern from above. The product of the subtraction is once again equal to the vector created between the two ends of the diamond.

Scaling Vectors (Scalar Multiplication)

On the ACT, the only kind of vector multiplication that a student might be asked to know is scalar multiplication. Like the name suggests, this is simply scaling the vector up or down (either growing or shrinking it). There are ways to multiply actual vectors together, but this should not be covered on the ACT Math section.

Scalar Multiplication follows some quick and simple rules:

If a vector is multiplied by a number whose magnitude is greater than 1, then the vector will increase in magnitude (length) by that number

If a vector is multiplied by a number whose magnitude is less than 1, then the vector will shrink in magnitude (length) by that number

If a vector is multiplied by a positive number, then the direction of vector will not change

If a vector is multiplied by a negative number, then the direction of vector will be reversed

i and j notation

Vector problems sometimes use the variables iand j. These are known as the unit vectors, and each variable is associated with a specific axis. i is the unit vector for the x-axis. j is the unit vector for the y-axis.

When these show up on an ACT math question, they will often be used to refer to direction. For example, here is a sample question on vectors from an ACT Diagnostic test:

Since vector j represents 1 mile per hour north, that means that − j would represent 1 mile per hour south. Maria is jogging south at 12 miles per hour, meaning that − j would need to be scaled up by 12 to properly represent her velocity.

Therefore, the answer is 12 • − j = − 12j or B.

Worth Knowing (>25% chance):

41. Permutation

Permutation is similar to the counting principles discussed earlier. However, permutation questions involve options which are mutually exclusive.

Here is a sample ACT question involving Permutation:

Unlike with the security lock question covered above, once a plant is used in one display spot, it cannot be used in a different display spot. So instead of simply multiplying all of the possibilities together 6 * 6 * 6, now there is one fewer possibility each step of the way (since regardless of which plant is chosen, there will only be 5 plants to choose from for the second spot and 4 for the third).

The answers is therefore 6 * 5 * 4 = 120 or D.

Counting principle questions and permutation can intersect when there are limits introduced to the counting principle setup. For example, if the license plate example from above included the stipulation that no number or letter be repeated on a license plate, then the question would be similar to permutation. The number of options would reduce by 1 for each digit series (numbers or letters) that was continuously drawn from.

42. Volume of a prism

Simple Shapes

The volume of a simple 3d object is equal to the area of the base object multiplied by the height of the object

Volume of a cube: s³, where s is the side length of the any square side
Volume of a rectangle: l • w • h
Volume of a right cylinder: πr²h

Complex Shapes

The shapes above all have right vertices, meaning that their heights are consistently perpendicular. Not all 3D shapes have perpendicular vertices, which means that their volume equations are more complex.

The most likely weird volume equation to be asked about is:

Volume of a Sphere: $$\frac{4}{3}\pi r^{3}$$

Other strange area volumes that can be worth knowing:

Volume of a Right Cone: $$\pi r^{2}\frac{h}{3}$$

Inscribed Volume

One of the more complex volume problems to see on the ACT involves inscribed objects, meaning where one 3D object is inside of another. On the ACT this usually involves a sphere and a circle, either of which can be the interior or exterior object.

The first key to these questions is to draw it out. It will seem complex when it’s first described, but the calculation should become more intuitive once it is drawn out. The objects will have to be described as touching each other at at least one point, but most likely all points. This will then give key information about the relationship between things like the length of the sides of the cube and the radius of the sphere.

43. c = product of roots, b = sum of roots, a = scaling

When factoring an exponential equation (ax2+bx+c into (x-d)(x-e)), the signs and magnitudesof b and c can provide a lot of information that is useful for factoring.

Example Equation: x² + 3x − 10

C

C should always be the starting place any time a student factors. It gives direct and specific information about the constant terms of the pair of binomials that would be created by factoring,

C is the equal to the product of the two constants. This means that:

Magnitude: The magnitude of C is equal to the product of the magnitude of the two constants in the binomials
Sign: If the sign of C is positive, then the constants in the binomial have the same sign (two negatives or two positives). If the sign of C is negative, then the constants in the binomial have opposite signs (one positive and one negative).

In the example equation above, the magnitude of C is 10, meaning that the constants would be factors of 10. The sign of C is negative, which means that the constants have opposite signs.

B

B is equal to the sum of the two constants. Combining this with what is known from C:

If the signs of the constants are the same, then the sign of B is the same as the signs of both constants

If the signs of the constants are opposites, then the sign of B is the same as the constant with the larger magnitude (the bigger number regardless of sign)

A

A is the product of the coefficients in front of the variable terms in the binomials. Most ACT quadratic equations will not have a coefficient in from of the variable term (the coefficient will just be one), so B and C are the main things students should be comfortable with translating.

However, if the A term is something other than 1, it’s worth knowing the following things:

Normally A will be a perfect square: 1, 4, 9, 16. Meaning that the signs in front of the variable term will be the same in each binomial.
If A is not a perfect square: It will usually be an odd, prime number such as 3, 5, or 7, as then the coefficients in front of the variables have to be that number and 1.
A does not affect C, but it will scale the terms that add up to B: since C is just the product of the two variable terms, it is not affected by coefficients on the x term. However, it will affect the variable terms that sum to b.
- If A is a perfect square, then the terms that sum to B will be scaled evenly
- If A is not a perfect square, then one term will be scaled by a larger factor than the other.

44. Circle equations

The default equation of a circle looks like this: (x−h)² + (y−k)² = r² where r is the radius of the circle, and the x and y binomials indicate where the center of the circle is.

The sign inside of the equations will be the opposite from how the circle moves from the origin. (x-3)means that the center of the circle is located at x = 3, rather than x = -3.
This is true for both the x and y portions of the equation, rather than just the x term

Circle questions on the ACT math section will normally provide either a graph or an equation. Whichever one is provided must be used to find the one that isn’t provided.

45. Difference of two squares

Difference of two squares is a pattern that can be used to factor certain quadratic equations on the ACT math section. The default formula is that:

a² − b² = (a+b)(a−b). The terms in this formula can be either variables or constants. There is no center term because the two binomials are conjugates of each other.

When the difference of squares appears on the ACT, the a term is normally a variable and the b term is a constant. This means the left side of identity normally looks like: x² − 16.

46. Arithmetic sequence

Arithmetic sequences are similar to function, in that they indicate a way to work with numbers. However, instead of working with numbers continuously (including terms with decimals), sequences work only with whole numbers.

Questions will normally provide a sequence, which students will then have to determine a specific term in (for example, the 27th term in the sequence). However, students can also be given numbers from the sequence and asked to identify a formula that could be the sequence those numbers follow.

Here is an example question from the 2017 April ACT:

Here the question is looking for the 50th term in the sequence. The 3rd and 4ths terms of the sequence are given. Since there is no other information, the sequence likely has to be something quite simple.

There is an increase of 5 in between the 3rd and 4th terms, so the sequence might be: n_x = 5 + n_x − 1, where x_n is the current number of the sequence and x_n − 1is the previous number in the sequence.

Since the sequence increases by 5 every term, and there it will take 46 more terms to get from the 4th term to the 50th, that means the 50th term will be 46 x 5 = 230 greater than the 4th term.

Therefore the 50th term is 4th term + 230 = 18 + 230 = 248. So the answer is A.

47. Laws of Sines and Cosines

The Laws of Sines and Cosines are useful for geometry questions involving non-right triangles.

Law of Sines

The Law of Sines states that $$\frac{a}{Sin(A)} = \frac{b}{Sin(B)} = \frac{c}{Sin(C)}$$ where a, b, and c are the side lengths of the triangle, and A, B, and C are the internal angles opposite those respective sides, respectively.

Questions involving the Law of Sines or Law of Cosines will not normally involve calculating a specific number. Instead, it will often be about plugging numbers into the equation, and then isolating a variable in that equation.

Here is a sample question using the equation:

This is a perimeter question. Since there needs to be a firefighter every 4 meters, the perimeter will need to be divided by 4 to calculate the number of firefighters needed. This eliminates answer C, since it is the only answer not divided by 4.

Answers D and E can also be eliminated, since they utilize an area equation rather than calculating a perimeter.

So the answer must be either A or B. This also makes sense, since the perimeter sum should include 130 meters, as well as the lengths of the other two sides (which will be calculated using the law of sines, so having the two angle ratios for the other two sides makes sense).

For this triangle, the Law of Sines would look like: $$\frac{130}{sin(91)}\ = \frac{b}{sin(47)} = \frac{c}{sin(42)}\ \frac{}{}$$.

So the lengths of b or c are equal to $$\frac{130}{sin(91)}$$multiplied by the sin of their opposite angles. So the correct equation should have sin(91) in both denominators and then sin(42) and sin(47) multiplied by 130 in each numerator. So the correct answer is A.

Law of Cosines

The Law of Cosines is similar to the Law of Sines, but rather than comparing individual ratios of each side/angle pair it includes all:

c²= a² + b² − (2ab • cos(C)).

48. Triangle opposite side rule

The sides of triangles and the angles opposite them are related and this relationship may be useful on certain triangle questions.

The most important thing to remember is that the length of the side of a triangle is proportional to the angle opposite that angle. So the largest side will also have the largest angle opposite it.

This is why the hypotenuse of a triangle always has the 90 degree angle opposite it in a right triangle.

49. Change the base – If 9^x = 27^5, what is x?

Some questions will require changing the base of a number with an exponent. For example,

16^x = 256⁴, then what is x?

256 = 16² , meaning that the original equation can be rewritten as 16^x = (16²)⁴ = 16⁸

This will usually involve numbers whose square or cube roots are simple integers.

So it’s useful to get familiar recognizing the first few numbers in these exponent sequences:

Number	x²	x³	x⁴
2	4	8	16
3	9	27	81
4	16	64	256

50. Similar triangles

Similar triangles are triangles that have the same angles, but different side lengths. The easiest way to think of this is to imagine a triangle being scaled up or scaled down.

With similar triangles: angles are the same but side lengths are different

To maintain the same internal angles, the ratio of the sides of similar triangles has to remain consistent.

If specific numbers aren’t given for a similar triangles problem, then it’s best to look at the shape of the triangle.

If the original triangle has relatively equilateral sides (is roughly symmetric) then a similar triangle will have to be similarly symmetrical. If the original triangle looks stretched to one side or very flat (long base and long sides), then the similar triangle has to be the same as well.

51. Probability with “not”

Probability questions with not are similar to normal probability questions. The main difference is that the odds that need to be calculated are the odds of failure rather than success.

In the earlier examples on probability, the focus was on drawing a specific color of starburst out of a bag. The odds there were simply: $$\frac{\#\ of\ starbursts\ of\ that\ color}{\#\ starbursts\ in\ total}$$

If the question were changed to “what are the odds of drawing a color that is not red out of a bag of starbursts”, then the odds are simply equal to: $$\frac{\#\ non – red\ starbursts}{\#\ total\ starbursts\ in\ the\ bag}$$. So instead of adding up the red starbursts, add up all of the other colors.

Another way to think about it is that the probability of something not happening is equal to: 1 − P_s where P_sis defined as the odds of that same thing happening. Since probability is just a likelihood out of 1 (or 100%), the odds of success and failure always add up to 1. So a student can also simply calculate the odds of success, and then subtract that from 1.

52. Factors

Factors refer to numbers that can be multiplied together to reach a specific product. For example, 2 and 3 are factors of 6 because their product is 6. Quadratic factors were discussed above, while this section will focus on whole number/constant factors. These types of factors usually come up on the ACT in the following ways:

Greatest Common Factor

Similar to the Least Common Multiple expressed above, the Greatest Common Factor is the largest factor that is shared between a set of numbers.

So instead of looking for the smallest number that every number in the set factors into. Now, the goal is to find the largest number of the factors into the numbers in the set. Put another way:

Least Common Multiple looks at the set of numbers as factors
Greatest Common Factor looks for factors of the set

For example, the Greatest Common Factor of the set: 12, 24, 42 is 6, because it is the last whole number that divides evenly into all numbers of the set.

Prime Factorization

Some Greatest Common Factor questions will ask about the concept of Prime Factorization.

Prime Factorization means factoring a number using only prime numbers. In other words, figuring out what prime numbers need to be multiplied together to reach a given number.

For example, the prime factorization of 60 would look like this: 5•3•2•2

To get the prime factorization of any number, factor it normally, and then keep factoring until all of the numbers in the sequence are prime. Regardless of which factors you start with, the end product will be the same.

60 = 20 • 3 = 5 • 4 • 3= 5 • 3 • 2 • 2

60 = 15 • 4= 5 • 3 • 4= 5 • 3 • 2 • 2

53. Trapezoid

Trapezoid questions on the ACT usually relate to the area of the shape or the internal angles of the shape. As a result, it’s worth knowing that the area formula for a trapezoid is:

And that a trapezoid has 360 degrees of internal angles inside of it.

54. Domain and Range

Domain and Range are two common terms used in reference to functions and data sets, respectively.

Domain refers to the set of all possible values of x for a given function
Range refers to the distance between the highest and lowest numbers in a data set, OR it can also refer to all of the possible output (or y) values for a given function
- When referring to a data set, the range is one, discrete number: “The range of the data set is 36”
- When referring to a function, the range will be a set of all possible outputs of the function

55. Conjugates

Conjugates are binomial pairs that have the same numbers/variables within them, but opposite signs. So for example (x-1) and (x+1) are conjugates. Conjugates have special properties that can be useful to know when they appear in questions or answers on the ACT.

Simplifying and Rationalizing Denominators

This particularly true when the original denominator contains either a radical (square root) or imaginary numbers (i = sqrt(-1)).

For instance, if the fraction $$\frac{5}{10 + 3i}$$is given, then this can be multiplied by $$\frac{10 – 3i}{10 – 3i}$$(standard algebra rule: multiplying it by one does not change the value of the fraction).

This leads to the fraction: $$\frac{50 – 15i}{100 – 3i^{2}}$$. i² = − 1, so − 3i²= + 3. So the denominator of the fraction can be simplified to 103, giving the final fraction $$\frac{50 – 15i}{103}$$.

Imaginary roots of polynomials always come in conjugate pairs. So whenever you see a binomial that includes i, think conjugate.

Conjugates and Quadratics

When conjugates are factors of quadratic equations they cancel out the middle terms of the equation and leave only a² + c. Whenever this equation appears in a problem, it means that the equation can be factored into a conjugate pair.

56. Exponential Growth/Decay

The Exponential Growth/Decay formula is one of the most common equation forms to see on the ACT. It can be used to express a multitude of different situations, which means it can show up theoretically as a variable function or practically within a word problem. The formula looks like this:

Final = Initial (1±growth/decay rate)^time

Key Takeaways

If it is a growth function, then the number inside of the parenthesis should be greater than 1

If it is a decay function, then the number inside of the parenthesis should be less than 1

Final is the output of the equation. It is like the y-value in a linear equation. It is the thing that is being calculated

Initial is the starting point of the equation. It is like the intercept in a linear equation. It says what the starting point is for the equation.

T is usually the main variable in the equation. It says how long the equation needs to be run for (how many cycles it goes through), as well as how often it will happen.

How It Shows Up In Problems

Exponential growth and decay problems are often word problems. The problem will describe an example of a real-life situation that utilizes this formula. The problem will then either:

Present the correct version of the formula, and then ask students to interpret one element of the formula

Give several different possible iterations of the formula, from which the student must choose the correct version of the formula as described in the problem

Common Exponential Growth/Decay Formulas or Questions

This formula can be applied to a wide variety of situations, but there are a few variations of it that have shown up on multiple exams and are therefore more likely to show up on any given exam.

Financial/Compound Interest

The compound interest formula shows how an investment growths with time. The exponent is normally equal to the number of years that the investment grows for or the number of months divided by 12.

Final = Initial (1±interest rate)^years or $$Final\ = \ Initial\ (1 \pm \text{interest\ rate})^{\frac{\text{months}}{12}}$$

Half-Life

The “half-life” says that after X number of years, the amount of a given element remaining will be half of what was initially there. This is why the rate inside of the parenthesis is $$\frac{1}{2}$$and the exponent will be equal to $$\frac{\text{number\ of\ years\ elapsed}}{the\ half – life\ (in\ years)}$$.

$$Final\ = \ Initial\ (\frac{1}{2})^{\frac{\#\ years}{half – life\ years}}$$

Doubling

The doubling formula is the same as the half-life formula, but with a two inside of the parenthesis and where the denominator of the exponent is the time it takes to double rather than the time it takes to halve. This can be expressed in years, but is often expressed in smaller units like hours.

$$Final\ = \ Initial\ (2)^{\frac{\text{time}}{\text{time\ to\ double}}}$$

57. Weighted average

Weighted averages are a way to combine the averages of two data sets of different sizes. This is similar to calculating sum totals on a histogram.

For example, two classes are described. Class A has 10 students who had an average test score of 75. Class B has 15 students with an average test score of 90. A question might then ask what the combined average of the two classes is.

The most basic way is to simply calculate the total scores of both groups: number of students • average score, and then add those two totals together and divide by the total number of students.

(75 •10) + (90•15) = 750 + 1350 = 2100 $$\frac{2100}{25} = 84$$

The other way to do this is to take the ratio of the two numbers of students, and then weight each of the averages according to that ratio.

$$\frac{\#\ Students\ in\ Group\ A}{\#\ Students\ in\ Group\ B} = \frac{10}{15} = \frac{2}{3}$$ There are 2 students in group A for every 3 students in group B. Multiply both averages by their weights in the ratio, and then divide by the total number of students within that ratio.

(75•2) + (90•3) = 150 + 270 = 420 $$\frac{420}{5} = 84$$

The math is the same as above, but scaled down by a factor of 5, which makes the numbers a bit easier to work with.

Finally, one can also take the ratio numbers, and use them to calculate which portion of each average should be used for the weight average.

Group A weight = $$\frac{2}{5}$$ Group A Weight * Group A Average $$\frac{2}{5} \bullet 75 = 30$$

Group B weight = $$\frac{3}{5}$$ Group B Weight * Group B Average $$\frac{3}{5} \bullet 90 = 54$$

54 + 30 = 84

Any of these methods yields the same number, so students should choose whichever seems most easy or intuitive to them.

58. Reciprocal vs. Inverse trig

Reciprocal Trig Functions

The normal trigonometric functions are sine, cosine, and tangent. However, there are also expressions for the reciprocals of these functions.

These functions are secant, cosecant, and cotangent. They are equal to the reciprocals of the ratios from SOHCAHTOA:

$$Secant\ = \ \frac{1}{\text{Cosine}} = \frac{\text{Hypotenuse}}{\text{Adjacent}}$$ $$Cosecant\ = \frac{1}{\text{Sine}} = \frac{\text{Hypotenuse}}{\text{Opposite}}$$ $$Cotangent = \frac{1}{\text{Tangent}} = \frac{\text{Adjacent}}{\text{Opposite}}$$

The easiest way to remember this is that for sine and cosine, each pair should have one S and one C. So Secant and Cosine are paired and Cosecant and Sine are paired. Cotangent and tangent are generally much easier to remember, as they are the only identities that have a T in them.

How It Appears on the Exam

The reciprocal trig functions are generally used in right triangle problems. This means they are used just like in a normal SOHCAHTOA problem, but where the ratios are inverted.

More rare problems will involve looking at graphs of these functions. The important thing to remember is that just like their functions, their graphs will also be the reciprocals of the sine and cosine graphs (cotangent graphs are not likely to come up).

Sine there are points where sine and cosine are = 0, these graphs have vertical asymptotes at those points. This is why the graphs of these functions look like this:

Inverse Trig Functions

Inverse trig functions are how to calculate angles from the SOHCAHTOA ratios

They are written using the normal trig functions, but with negative exponents: sin⁻¹, cos⁻¹, tan⁻¹

Since $$sin(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}}$$, $$\text{si}n^{- 1}(\frac{\text{Opposite}}{\text{Hypotenuse}}) = \theta$$, where θis the angle of the triangle with those opposite and hypotenuse sides.

Problems using the inverse trig functions generally will not ask a student to actually calculate a numerical value for the angle. Instead, students will simply be asked to understand how the inverse trig functions are applied to find an angle measure.

59. Parallelogram

Parallelograms are an important thing to review for the ACT, because they tend to be something students are less familiar or comfortable with. Problems involving parallelograms can therefore become an easy place for students to lose points. Some key things to remember about parallelograms are as follows.

Adjacent Angles

Adjacent angles in a parallelogram are supplementary, meaning that they add up to 180

Area Formula

The area of a parallelogram has the same formula as a rectangle: A = bh, but because it’s vertical sides are not perpendicular to the base, the height is not equal to the length of the side of the shape.

The area of a parallelogram is equal to the shape’s base multiplied by the height of a vertical line drawn from the shape’s top left corner down to the base

This is similar to finding the height of a non-right triangle, where the height has to be created by dropping a vertex down to the base.

60. Use the radius

Any time a circle appears in a problem, the first thing to think about is the radius of the circle. It is the core piece of information about the circle, and it is the thing that is most commonly used to calculate or infer information about things that appear in the rest of the problem.

The radius might be given numerically, but sometimes it can be given in a problem without an actual numerical value attached to it. For example, this is a problem from the December 2020 ACT.

Here it is not necessary to calculate the value of r, but instead simply to understand the relationship between each circle’s radii. The first circle has a radius of r, the second circle has radius of 2r, and the third circle has a radius of 3r.

The perimeter function for a circle is 2πr. Therefore, the sum of the circumferences of the circles is 2πr + 2π(2r) + 2π(3r). This can be rewritten as 6(2πr). The question said that the circumference of the smallest circle is 10, and since the circumference of the first circle = 2πr, then 6(2πr) = 6 • 10 = 60. So the answer is G.

61. Value/frequency charts

Frequency charts summarize data sets by showing how often each data point appears within a set. This can be displayed as either a table or a graph. Questions about these charts will generally focus on the mean/median of the data set.

Students should be comfortable calculating the mean/median from either of these two types of charts. Like other mean and median questions, ACT questions will often ask about what would happen to the mean/median of the data set if a new number was added or if a previous number was changed.

62. Pythagorean Triples

There are a few common triangles that appear on the ACT math section that are called “Pythagorean Triples”. These are right triangles where if a student knows two of the sides, they also can know the third side automatically without having to use the pythagorean theorem. These triangles are known as 3,4,5 and 5-12-13 triangles.

The key for these triangles is to remember that the largest number has to be the hypotenuse for these to be true. So if a triangle has side lengths 5 and 13, but they are the two shorter sides, then it is not a 5-12-13 triangle.

These pythagorean triples remain true even when the numbers are scaled up by any given integer. So, when 3,4,5 becomes 6,8,10 (each original number multiplied by 2), it’s still a pythagorean triple. As long as the proportions remain consistent, the relationship remains true for these types of triangles.

63. Lowest Common Denominator

The Lowest Common Denominator is the smallest number that can be a denominator for two separate fractions. Another way to think of it is that it’s the smallest number that both original denominators can factor into. This is why the most common way to find the LCD is simply to multiply the two denominators together. For example:

$$\frac{1}{2} + \frac{4}{5}$$ 2 • 5 = 10 That makes 10 the lowest common denominator.

To get both fractions to that form, multiply them by the opposite denominator divided by itself. In the above example, that means multiply $$\frac{1}{2}$$by $$\frac{5}{5}$$. Since anything divided by itself = 1, that means the fraction is not being changed, only scaled.

The above equation thus becomes: $$\frac{5}{10} + \frac{8}{10} = \frac{13}{10}$$

64. System of equations with three equations

Most systems of equations problems only involve two equations, but occasionally they’ll include three equations, often in the form of a word problem. For these problems, students need to isolate two different variables in two of the equations. These then need to be substituted in for each other in the 3rd equation.

The main key is that at some point all of the variables in the equation will need to be substituted or eliminated until only one variable and a constant remain.

For example:

3x + 2y − z = 6

− 2x + 2y + z = 3

x + y + z = 4

65. Compare numbers

Some questions on the ACT math section might require comparing the size of numbers expressed in different forms, or where the expressions contain only variables.

For these questions, it’s important to remember simple things about different expressions:

Radicals/Square Roots: The equivalent/value of a square root gets large as the number under the root/radical gets larger, but it does so at a decreasing rate. So going from 1 to 4 (an increase of 3) leads to a doubling of the equivalent value: = 2 vs. = 1.

However, going from 49 to 52 (another increase of 3) leads to a much smaller increase in equivalent value: = 7 vs. = 7.211 .

x^a Exponents: Larger exponents make larger numbers. Each increase in a positive exponent leads to an even larger growth in the number affected (increases at an increasing rate).

Negative exponents do the opposite. Negative exponents lead to smaller numbers and the numbers will shrink at an increasing rate.

$$\frac{a}{b}$$ Fractions: The larger the numerator and the smaller the denominator, the greater the value of a fraction will be. The smaller the numerator and the larger the denominator, the smaller the value of the fraction will be.

.abcde Decimals: The leading digits of decimals determine their relative value. If the first digit of a decimal has a greater magnitude than the first digit of another decimal, then the first decimal has a larger overall value, regardless of the following digits. If the first digit or first several digits are the same, then the relative size of the decimals is determined by the first non-shared digit in the decimals.

|a| Absolute Value: Absolute value is about magnitude, so the further away the digit inside the square root is from 0 (regardless of its positive or negative), the larger the equivalent value will be.

Sample Question

P is a positive number. n is a negative number, and p has a greater magnitude than n. The question wants the biggest number possible. All of the answers are inside of an absolute value, meaning that the largest number will be the fraction that results in the furthest magnitude away from 0.

Looking at the answers:

F and G: These answers have the same numerators, but different denominators. P > n, so the numerator is positive. P > n, so the denominator is greater in F. A larger denominator means a smaller magnitude, so G has a greater value than F.

H, J, and K: These answers all have the same numerator, but different denominators. K’s denominator (n) will be the smallest, since n is a negative number smaller than p, which means that p-n > p and the magnitude of p is greater than the magnitude of n (again, absolute value means that magnitude is the important measure).

G and K are the last two options left.

They are the same, except for their numerators. The question wants the largest value. Bigger denominator = larger value. Since n < 0 and p > 0, (p − n) > (p+n). Therefore, G has the largest denominator and thus the larger value.

66. Translations

Translation questions will involve moving a shape or the graph of a function in one of three ways: translation, rotation, or reflection.

Translation

Translation: the orientation of the shape or graph will not change, but it will move to a new space in the xy-plane.

Rotation

Rotation: the shape or graph will be rotated about the origin. This means that the origin will be the center of rotation, so whichever point of the graph or shape is closest to the origin will remain closest to the origin, but it will likely change to a new quadrant of the xy-plane.

Reflection

Reflection: the shape or graph will be “flipped” along the y-axis or x-axis. Another way to phrase this is that a reflection creates the “mirror” image of the shape/graph on the other side of the axis that it is being reflected along.

67. Stem and Leaf Plots

Stem and leaf plot questions are a way of displaying a set of data in a concise manner. The name refers to the fact that the leading digit (usually the tens digit) is removed from each data point, and instead is used as a label for a row that includes all data points with the same tens digit.

Stem and Leaf Plot questions will look like this:

The important thing to remember is that each “leaf” represents a different data point, while the stem only refers to their tens digit.

The question asks about students who jumped at least 60 inches, so for data points ≥ 60. There are 5 students in the 6-stem row and 3 students in the 7-stem row. This means that 8 students had a score of at least 60, out of a total of 19 students.

The odds are therefore $$\frac{8}{19}$$, so the answer is K.

68. Converting Angles to Radians or Vice Versa

Angles within a triangle can be expressed one of two ways. This can either be in degrees or radians.

Each circle contains 360 degrees or 2πradians

Therefore to convert between the two:

Converting from degrees to radians: multiply by π and divide by 180
Converting from radians to degrees: multiply by 180 and divide by π

69. Factorials

Factorials express a product of multiple consecutive integers starting at 1. Factorials look like an exclamation point, which is placed next to either a variable or a whole number. However, even when placed next to a variable it still indicates a whole number reached by multiplying that variable by all of the integers before that variable.

So 4! = 4 • 3 • 2 • 1 or x! = x • (x−1) • (x−2)….. • 1

The main trick with factorials is to remember that when they are divided by each other, the smaller factorial will divide out and the remainder will be the product of all remaining integers from the larger factorial.

For example, $$\frac{17!}{14!}$$=$$\frac{17 \bullet 16 \bullet 15 \bullet 14 \bullet 13… \bullet 1}{14 \bullet 13 \bullet 12…}$$= 17 • 16 • 15. So even though the fraction is being “simplified”, it is the larger numbers that will remain rather than the smaller numbers.

Since factorials are products, the above rule is true regardless of whether the larger number is in the numerator or denominator (it just determines where the remainder goes).

70. Faces on a 3D Figure

The ACT sometimes likes to include questions that involve 3D objects that have a number of faces on the object. The faces on the object will be common geometric shapes such as triangles, squares, or occasionally more complex shapes such as hexagons.

Key things to remember for faces on 3D figure questions are:

Shared Edges: Faces on the shape will have shared edges. Each edge will be shared by two faces, and each face will have the same numbers of edges as it has sides.
Area: the area of the shape is equal to the summed area of all of the individual faces

Here is a sample question from the April 2017 ACT:

There are 20 sides to the die, each of which has 3 edges. Each edge is shared by two faces. Therefore the number of sides = $$\frac{(20 \bullet 3)}{2} = 30$$. The answer is D.

71. Step Function

A step function is a function that includes a series of horizontal lines, which jump from one to the other at regular intervals.

A step function graph will include open and closed dots. These open and closed dots pairs are where the function “jumps”
The jumps will usually occur at whole number values of the x-axis

Here is an example question from the 2017 ACT:

For ABC cabs, the price of a taxi fare jumps $2 each time the fare reaches a new whole number value. This means for any distance of less than 1 whole mile, the fare is $2. As soon as 1 whole mile is reached, the price then jumps to $4. It stays at that price until 2 full miles are reached, and so on.

The prices on the Y-axis are flat fares (they are not per mile). So to compare the price of a 5-mile fare for each company, a student must simply compare the y-values at x = 5 for both companies. For a 5-mile trip, ABC will charge $12 and Tary will charge $9. Therefore, the cheaper fare is $9.

Bonus: General Math Problem Advice

Things to Do With the Questions

Simplify

Sometimes an equation will be given in an unsimplified form. If a formula is given unsimplified, the first thing to do is to simplify it. The question is not written that way by accident, it’s done to make the problem seem more challenging or harder to solve. Once it’s been simplified, there is a good chance it will look more familiar or more manageable than it did in its original form.

Pull Out the Numbers

This is especially a good idea for word problems that seem confusing on first read. Remember that some words in word problems aren’t useful mathematically, and others are only useful when translated into something actually mathematical. Pull out numbers, variables, and any mathematical statements of fact (relative sizes, positive/negatives, sample sizes, etc).

Draw it Out

Especially true for graphing questions or word problems (especially if they seem to involve some kind of geometry).

Things to Do With the Answers

Look at the Answers

If all of the answers have a certain denominator or include a special symbol (like a square root or negative), then that says the question revolves around that concept. Or that one needs to take the number/formula that is originally given and convert it to look more like the answer choices.

Plug in Answers

This should be done when a student doesn’t know how to approach a problem conceptually. It’s important to remember that it can take a fair amount of time, depending on how complex the problem/equation given is.

Eliminate Answers

It’s never optimal to have to guess, but if one has to guess, then it’s best to give oneself the greatest odds possible of getting things right. When there are five possible answers, even eliminating two wrong answers can improve the odds of guessing correctly from ⅕ to ⅓.

It’s easiest to eliminate answers in batches. For example, if a student knows that the number has to be positive to be correct, then all of the negative answers can be eliminated. Same is true for if the answer needs to be even or to have a certain denominator.

Boost Your ACT Math Score With SoFlo Tutors

Getting comfortable with these 71 concepts is a great start towards being successful on the ACT Math section. But there is always more to be done to be prepared, both for the math section and the English, Reading, and Science sections as well.

This can seem intimidating to do alone, and that’s why SoFlo Tutoring offers smart, reliable, and helpful tutoring services that are personalized for each individual student. High-scoring, expert tutors can help anyone to set goals, practice problems and concepts, and put themselves in the best possible position to be successful. Schedule a free consultation with SoFlo today for help on the SAT or ACT!

SoFlo SAT Tutoring

5.0

Based on 109 reviews

review us on

Christa Bowden

14:02 08 Oct 22

I cannot say enough good things about SoFlo tutoring. They were so much more targeted and helpful for ACT prep than the official ACT prep course that my son took. When he did not gel with his first SoFlo tutor, they immediately switched him to one with whom he worked extremely well. He was able to... raise his ACT score 5 points between the July and September tests, and I think that this was in large part due to the exceptional work that his tutor Kai did with him over five weeks to target his practice and prepare him to do his best on the test.read more

Michelle Udeshi

17:12 27 Jul 22

We have been extremely pleased with SoFlo tutors so far. They worked with us to find a tutor who would be the best match for my daughter, given her learning style and goals. She has learned effective strategies to maximize her ACT score, which has improved significantly in a matter of a few weeks!... After considering other tutoring options, we are happy we chose SoFlo!read more

Aween Ali

02:22 14 Jul 22

Casey Jang is an amazing tutor. She is really helpful, kind and understanding. I would reccomend her to anyone who wants to improve their SAT score.

Penny Schiano

21:27 05 Jul 22

This is the exact SAT prep which I wanted for my twin daughters! They only spend their time reviewing what they need to work on! The girls love the individualized instruction tailored to their specific areas of need. Highly recommend!

Alexandr Levin

18:42 04 Jul 22

Very knowledgeable and educated SoFlo tutors. My daughter has been received a lot of useful information and increased her score.

Christi Lehner

21:39 15 Jun 22

So glad we found SoFlo after trying many other programs to support our daughter doing her very best for her future. The tutors are bright, relatable and genuinely invested in their students success.

Nelly V. Таcheva

18:55 02 Jun 22

Thank you so much for your help, SoFlo team! Everyone has been super responsive, helpful, and caring.My daughter was able to improve her SAT score to 1500!

Audrey Bachmann

15:24 26 May 22

I have only had tutoring for almost two months, and my SAT has already went up 100 points! I am exited to see how much I can improve. This has helped me so much and I appreciate the support!

Rylie Saffles

02:02 11 Mar 22

The tutors are so nice, and they help out so much! I most definitely recommend this company! I am a high school student taking the SAT again for scholarships, and this company has helped so much!

Suzana Marks

12:24 03 Mar 22

My son was tutored for a bit over 2 months before taking the SAT in 11th grade. He needed assistance with math.This was a worthwhile experience, as my son felt that he was absolutely more prepared for the test.The price per hour is more than fair and incremental hour billing is an outstanding... option.I highly recommend SoFlo for your tutoring needs.read more

Tracy Sargent

16:35 26 Feb 22

My daughter had a terrific tutor from SoFlo tutors. My daughter needed a tutor for college statstics. She worked with the SoFlo tutor who is a Harvard student and my daughter's test scores went from in the 70s to in the 90s.

Annette V

18:39 06 Feb 22

I am so happy we found SoFlo SAT tutoring! We researched in great depth to find the best option for our son and SoFlo does not disappoint. We were sent a diagnostic test so that they know exactly which areas need improvement. Kenneth, my sons’s tutor is absolutely wonderful. Each week he goes over... important information and assigns homework. He makes sure to focus on information my son doesn’t fully understand. He is always so patient and kind, which helps make learning a joy. My son throughly enjoys his weekly sessions with Kenneth and is always so excited when he has learned a new concept. Kenneth and the administrative team at SoFlo are excellent with communication and letting me know how everything is going.read more

Monica Cooke

16:01 25 Jan 22

My son is working on meeting his reading graduation requirement on the ACT and/or SAT. He has been tutoring for 3 weeks and seems to really like his tutor Kenneth. Test is still a few weeks away but he is feeling extremely confident and that is truly a plus. We cannot wait to see his test scores.... Thank you Kenneth for all your help so far!read more

Theo Ma

15:12 31 Dec 21

SoFlo Tutoring is also ideal for already high scoring students. Before I began tutoring, my best SAT score on a practice test was a 1450, but after tutoring, my scored increased by over 100 points to a 1560 on the actual SAT. My tutor, Jack, was very knowledgeable, and he gave me a lot of good... advice, especially on the reading section of the test. Ultimately, I am very glad that I found SoFlo Tutoring and very thankful for their help in boosting my score into the 1500s range.read more

Emma Kutcher

19:24 14 Jul 21

This is the first review I have ever written on Google, and I'm happy to be doing it for SoFlo tutors. As a student working to improve my SAT score and begin applying to college, I have received the best possible resources and services here. My tutor, Manuela Penenory, has been so amazing and... supportive and helped me to improve my score by 100+ points. She is so kind and always willing to discuss and answer any questions I have about the SAT, college applications, extracurricular involvement, etc. Christina Meyer has also been so supportive and helpful with providing resources for me as a lower-income student. I am so grateful that she has taken the time out of her day to schedule calls with me to discuss college applications and resources I need to improve. Both of them are so so amazing, and I am so happy that I found SoFlo. :)read more

Haley Johnson

23:27 26 Jun 21

SoFlo SAT Tutors is an amazing program that will help students achieve the score they wish to get

S Silva

02:57 29 Apr 21

SoFlo was an ideal fit for our son. Adam and his team quickly assessed PSAT and PreACT performance and developed a plan focused on the ACT. Hunter is a fantastic tutor and created an immediate connection; his weekly online sessions were highly efficient and effective, keying on specifics... strategies while instilling confidence and allowing more time for practice exams. Six weeks after the first conversation with SoFlo, our son scored a 34 on the ACT. Exceptional tutoring at an exceptional value! Thanks Adam & Hunter!read more

Grace Lawson

01:56 28 Apr 21

Jenny was my tutor and she was absolutely amazing at it!! Only two weeks of tutoring and I improved my ACT score by 3 points!!

Braydon Kent

21:15 31 Mar 21

Aakash Margam is the tutor you want, he explains everything almost perfectly and will have you shake your head as he tells you the answer. He doesn't use tough speech so it's really easy to understand him and he is also very friendly and open-minded. The tutor you want is Aakash Margam.

Ashley Borel

09:06 12 Feb 21

I look at my journey to pass the bar as a cumulative process. Each study day and bar exam attempt was a step closer to victory. I took the bar exam 4 times before I was victorious. Choosing SoFlo SAT Tutoring was an important step toward my victory.

Alexandra Young

12:38 10 Feb 21

I would still be languishing in pre-passing purgatory. They created a customized study strategy that addressed my specific needs. The one-on-one meetings and reviews of my essays proved enormously helpful. Slowly but surely and I corrected the flaws in my writing and more importantly, changed... my approach to essay writing.read more

Natalia Nayali

01:53 08 Dec 20

I really like Soflo SAT tutoring. My daughter has improved 100 in her SAT scores. Also her tutor in very responsive and smart and kind. I also think their customer service is great. I would recommend them blindly !!

Luis Carlos Fonseca

01:32 08 Dec 20

I am confident this is a great option for my daughter

Tara Henry

20:45 07 Dec 20

We've truly had a wonderful experience with SoFlo. My daughter actually 'enjoys' her tutoring sessions - crazy!! After just a couple sessions her PSAT score increased by 80 points.

Mindy Wright

14:59 26 Aug 20

I don't typically write recommendations because it is perception and every child is different….but I am one privileged parent to have found SoFlo Tutoring for our son, a Junior in high school...he has had a great learning experience. The tutors at SoFlo are highly qualified in the subjects they... teach and are extremely skilled in conducting the classes, via Zoom for us. Financially affordable and in-line with other tutors. Christian Chase is an excellent SAT/ACT tutor and has superb “Math” and “English” skills which I have already seen a cross over into his school work. Adam was able to match our son up with Christian who is an excellent tutor…he is responsive, via text, email or phone. SoFlo is willing to go above and beyond to set up personalized tutoring, and Christian has been very flexible with our schedule which I appreciate! I received a call from my son's english teacher suggesting we move him to AP English, he is already dual enrolled and taking other AP classes...Thank you SoFloread more

Alice Cain-Moore

22:20 23 Dec 19

Great personalized service. My daughter improved her score by 100 points. My god daughter by 140 points. Better results than most of the other companies out there. Thanks Adam!

Leo Weisberger

19:24 29 Nov 19

I found SoFlo SAT Tutoring online and they left a strong impression. I had searched and spoken with many test prep companies but they were the best. They answered all my messages and respond to my calls very promptly. Also there were no contracts so I gave them a shot even though I had not heard of... the company before.The founder Adam was knowledgeable about SAT prep and friendly on our initial phone call and getting started was easy, just filling out a simple form. They had my son Greg take a diagnostic test to gauge his initial strengths and weaknesses. From the diagnostic we had a very strategic approach to prep and there were clear goals and direction.From there a polite young tutor reached out and began scheduling test prep sessions. My son is always very busy because he is on the soccer team, but our tutor Charlie was very flexible and scheduled sessions at my son's convenience. We met with Charlie once a week for two hours over the course of about 3 months. I was able to track my son's progress because he was always doing SAT practice tests for homework. His score was steadily climbing from week to week, and we were confident that he was going to improve his SAT score.After taking the SAT we decided to pause sessions thinking that we should wait until we see how Greg did on his test. Adam completely understood and did not pressure us to continue sessions. When the scores came out Greg improved over 200 points and scored a 1430 on the SAT. Tutoring is the best money I've ever spend and every step of the way SoFlo has been great to work with. I'm so appreciative!read more

Michael Light

21:48 18 Mar 19

SoFlo SAT Tutors got me into the garnet and gold for the next four years. With their help my ACT score went up to a 29 and I got the full bright futures scholarship. I recommend them to everyone and swear by their tutoring method. Adam’s tutoring is worth every single penny. The best ACT tutor in... South Florida! Go Noles!!!read more

HRiggott25

21:28 18 Mar 19

The best SAT tutor I could have ever imagined. I increased my SAT score by 260+ points and got into Johns Hopkins because of Adam and the SoFlo team. They know every trick to boost a score!!

Jake Samuelson

03:04 03 Mar 19

Adam Shlomi was an exceptional tutor and an expert when it comes to the SAT and ACT. I had visited college experts before and the general classroom approach did not improve the specific subjects I needed help with. Adam listened to all my needs and immediately formulated a plan to help me... strengthen my performance in the reading section. I met with Adam once a week for 3 months and he helped me improve my score by 120 points. I can’t thank him enough!read more

zach ames

05:29 23 Feb 19

The absolute best SAT tutor in Fort Lauderdale and Plantation. SoFlo Tutors boosted my sons ACT score by 7 points. They were super patient and thorough always making sure my son understood the concepts. They also fit with my schedule and tutored my son at our at house so I didn't have to drive him... to a test prep place. A great experience for college test prep, SAT tutoring, ACT tutoring, and college admissions advice. SoFlo SAT tutors are unbelievably good and I recommend them to everyone, worth every last penny!!!read more

More reviews

Just About Everything You Need to Know for the ACT Math Section

Which Topics are Most Important to Know for the ACT Math Section?

Must Know ACT Math Concepts

Extremely Likely Concepts

Very Likely

Worth Knowing

Must Know ACT Math Concepts

Fractions

Average

How It Will Appear on the Test

Probability

Key Takeaways

4. Percents

5. Exponents

Three Main Exponent Operations

Special Exponents

6. Linear Equations/Slope

Key Skills

Calculate Slope from Two Points

Isolate Y (Create y = mx + b)

Find Intercepts

Key Information for Linear Equations

Perpendicular Slope

“Real Solutions”

7. Solving Equations

Basic Skills

Distribute.

Combine like terms.

Special Skills

Creating Equations from Word Problems

8. Picking Numbers

9. Ratio

10. Quadratic skills

Leading Coefficient

Intercepts

Equations with Multiple Quadratics

11. Area/Perimeter of basic shapes

12. Negatives

Negative Operators

Negative Tricks

13. SOHCAHTOA

Sin and Cos Overlap

Word Problems

Extremely Likely (> 80% chance):

14. Function shifts

Vertical Shifts

Horizontal Shifts

15. Average sum trick

16. MPH

17. Median

Median of Odd-Numbered Data Sets

Median of Even-Numbered Data Sets

How It Appears on the Test

18. Radicals

Radical Operations

Cancel Out

Multiplication

Simplification

Division

Fractional Exponents

19. System of Equations

Two Methods for Systems of Equations: Elimination and Substitution

Substitution

Elimination

Deciding Between Substitution and Elimination

Look at the Numbers in the Equation

Look at the Question

Word Problems

20. Angle chasing

How Many Degrees in ______ ?

How Many Degrees in a Line

How Many Degrees in Common Shapes

How Many Degrees in Any Shape

Vertical/Opposite Angles

Angles at Intersections with Parallel Lines

21. Time

Time Conversions

Time Variables

22. Pythagorean Theorem

23. Apply formula