
Everything to know about geometry on the SAT, in one article!

What’s Covered in the SAT Geometry Section?
Whether it’s because it’s been a long time since they’ve taken a geometry class, or because they don’t enjoy working with shapes, students generally find geometry questions to be among some of the hardest topics on the SAT math section.
Luckily, geometry makes up a relatively small part of the exam, and by reading the following information, students will be more prepared.
First, students should know what geometry topics are covered on the SAT:
Area and Volume
These questions can ask students to find the area of a shape, or the volume of a solid object.
Area and volume questions should be relatively easier than other geometry questions because most of the area and volume formulas students will need are provided entirely on the reference sheet, so it’s just a matter of “plug and chug.”
Lines/Angles
These questions will typically ask students to find the value of an angle formed by intersecting lines. For these questions, students want to be familiar with the properties of transversals and parallel lines.
Circles
Circle questions can come in many different forms. Students may be asked about the area or circumference, in which case all the information students need is provided on the reference sheet. However, circles can also cover harder topics including central/inscribed angles, or the arc length/area of a sector of the circle.
Triangles
Like circle questions, triangle questions often cover a wide variety of difficult topics. Students should be comfortable with the different types of triangles (right, 30-60-90, and 45-45-90) triangles as well as with how to find side length and area of a triangle.
What’s Good About the Geometry Section?
Students are given a reference sheet
One of the few acts of kindness the test creators do for students on the SAT is provide a reference sheet. At the start of the math no calculator and calculator sections of the exam, students will always be provided with a reference sheet that looks exactly like this:
There is never variation in the reference sheet, so students can expect to see this exact reference sheet each test. While students don’t have to remember the exact formulas on the reference sheet, students should know what types of formulas are included so students can quickly refer to the sheet as students take the exam.
The geometry section is a small part of the test
Luckily, geometry makes up a very small portion of total questions on the two math sections. The CollegeBoard has said that of the fifty-eight questions across the two math sections, only six will cover additional topics in math.
The additional topics include geometry, trigonometry, and complex numbers. This means students can expect most of the math questions to cover topics students probably covered in an algebra class, and there’s no point in only studying geometry. Students will be better off dedicating their time to topics covered more frequently.
Geometry questions generally appear at the end of a section
The questions on the SAT math sections are organized in order of increasing difficulty. Relatively easier questions will appear at the start, and the relatively harder questions will appear at the end. Because geometry is considered to be one of the tougher topics on the SAT, geometry questions tend to appear towards the end of a section. This means most of the time given for the math sections can and should be spent on questions covering other topics, instead of worrying about one geometry question.
Most questions can be solved with more than one approach
Even if students not comfortable with their geometry skills, geometry questions can usually be solved in many different ways that don’t require advanced geometry knowledge. For example, let’s take a look at this question from the calculator section of CollegeBoard Test 3:
Approach 1: Let’s say a student’s goal is to get this problem done as quickly as possible, and they don’t mind using some geometry skills.
The example tells us sin(a°)=cos(b°). Building on that equation, it’s helpful to know going into the test that sin(a°)=cos(90-a°). Based on these two equations, they can say cos(b°)=cos(90-a°). Therefore, angle b is really equal to 90-a°.
They can now rewrite b=6k-13 as 90-a=6k-13, and then, after rearranging a few terms, rewrite it one more time as a=103-6k. At this point, there are two equations equal to a, the one they just figured out, and the equation given to us in the problem, a =4k-22.
Because there are two equations equal to a, students can set the two equations equal to each other, so that 103-6k = 4k-22. From here, solving for k will mean that k=12.5. The answer is C!
Approach 2: Let’s say the student doesn’t know how to solve this using geometry skills. No problem: they can use the answer choices!
From the information given in the problem, students know angle b should be larger than angle a, and both angles are acute, meaning that they both have a value of less than 90 degrees.
Begin by plugging in the answer choices as possible values for k into angle a. Quickly, they should realize that answer choices A and B are both wrong. Answer choice A will give a value of -4 degrees for angle a, which is impossible. Answer choice B will give a value of 0 degrees, which is also illogical.
Next, try plugging in answer choice C. Plugging in k = 12.5 for both angle a and b will mean angle a equals 28 degrees and angle b equals 62 degrees. Both of these seem like logical answers, so they don’t have to be eliminated right now — but students should make sure to check answer choice D as well.
When trying answer choice D as k = 21.5, angle a equals 64 degrees, which seems pretty logical, but that also means angle b equals 116 degrees. Based on this, students know answer choice D is also wrong because both of the angles must be acute. Therefore, by using only algebra, all answers can be eliminated except the correct one, C!
What Else Should Students Know for SAT Geometry Concepts?
The reference sheet is not all-inclusive.
There are many formulas and concepts not covered in the reference section that students may need to answer geometry problems. This means that compared to other topics in the math section, there is relatively more information students must memorize for the test.
Here’s a list of some of the most important formulas and facts to know for geometry questions:
Area of a sector
The reference sheet provides students with a formula to find the area of an entire circle. But what if the exam asks about the area of just one part of the circle? In this case, students would not use the formula for area of a circle, but instead would use the area of a sector formula. A section of a circle smaller than the whole is called a sector.
The formula is as follows: A = 360 r2, where ϴ is degrees of the sector. Notice how we are using degrees. If a question gives students an angle measurement in radians instead of degrees, simply convert to degrees using the formula given on the reference sheet.
For example, let’s say students are given a circle with r=5 and a sector with an angle of 60°. How would students find the area of sector x?
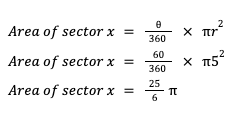
Length of a sector
Just like students can be asked to find the area of part of a sector, they can also be asked to find just part of the perimeter of a circle.
There is also a specific formula for the length of a sector: A = (π/180)(ϴ)(r), where ϴ is degrees of the sector.
If given radians, use this formula: A = rϴ, where ϴ is radians.
Let’s say that now, on my same circle, instead of figuring out the area of sector x, the question asks about the length. What equations should students be familiar with?
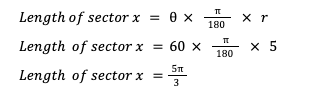
Central and Inscribed Angles
The SAT may give students the measure of an arc on a circle, and ask test takers to find the degree measurement of the corresponding angle, or vice versa. For these types of questions, it’ll be helpful to know some terminology.
Central angles are areas in the center of the circle. The point of the angle will be at the centerpoint of the circle. Inscribed angles are angles that extend throughout the entire circle. The point of the angle will be on the edge of the circle. An intercepted arc is the arc across the angle.
For central angles, the degree measurement of the angle is equal to the angle measurement of the intercepted arc. For inscribed angles, the degree measurement of the angle is half the angle measurement of the intercepted arc.
Based on these statements, students can also say that if a central angle and inscribed angle share the same arc, the degree measurement of the inscribed angle will be half of the measurement of the central angle.
Let’s take a look at a question from the calculator section of College Board Test 8:
In this circle, angle A is an inscribed angle, while angle P is a central angle. From the image, students can see angle A and angle P share the same arc. Therefore, angle P will have half the measure of angle A.
Because a relationship exists between angles P and A, students can start by trying to figure out the measurement of angle A. Notice how angle A is a part of the polygon formed by ABC. While the exact value of angle P is unknown, students can say that angle P = 360 – x because angle P and angle x will sum to 360°. It is also helpful to know that the sum of interior angles in a polygon is 360°.
Based on all this information, students can write the following equation: x2 + 20 + 20 + 360-x = 360. Solving for x will mean that x = 80°!
Sin(a°) = Cos(b°)
It is helpful to know that in a right triangle, sin(a°)=cos(b°) (and vice versa sin(b°)=cos(a°)). Angles a and b are acute angles that sum to 90°. Therefore, this equation can also be rewritten as sin(a°)=cos(90-a°) or sin(b°)=cos(90-b°).
Oftentimes, the SAT will give students the sine of one angle, and ask them to find the cosine of the complementary angle. If they know this equation, they don’t need to do any work to get the answer!
Take a look at this example from the no calculator section of College Board Test 1.
Earlier, we said sin(a°)=cos(90-a°). Therefore, without doing any mathematical calculations, students can quickly see the answer is ⅘!
How to Improve SAT Geometry Skills
SoFlo Tutors understand geometry is tough. For students who need help boosting their geometry skills, check out our excellent one-on-one tutoring services. Each student will be matched individually with a high–scoring SAT or ACT tutor and test expert who’s ready to help them improve their score.
Schedule a free consultation here!
About the Author
Ava Levine is a junior from New York majoring in International Studies at Johns Hopkins University. When she’s not in class studying various international issues, she enjoys learning about government policy and working with local nonprofits. She scored a 1570 on her SATs, is an avid Crocs-wearer, and loves to craft in her free time!










