
Out of all the sections on the SAT, students often feel the most stressed out and anxious when it comes to math. Math can be an intimidating subject, with numerous formulas to memorize, graphs to interpret, and rules to remember. Math, however, is a major part of the SAT, comprising of two whole sections. In order to ace the SAT, you need to feel confident and prepared to tackle the Math sections with your best shot!
Luckily, it doesn’t require nuclear physics to ace the Math sections of the SAT. Even if you’re more of an English or humanities person, you can still prepare in a way where you can totally ace the sections. It might take a bit more time, effort, and preparation, but, remember, the SAT is like any other test! The topics and types of questions are readily available to students, so nothing unexpected will be on the test if you adequately prepare for it.
If you struggle with math, or even if it’s your best subject, use this study guide to understand the structure and format of the SAT Math sections, learn or brush up on the topics tested, and discover how to create your own study plan.

About SAT Math
Before diving in to the nitty gritty of creating a study plan, it is important to first familiarize yourself with the structure of the SAT Math sections, the topics they will cover, and how you will be scored and graded. The first step to acing a test is to know its scope and format. It is only then you can tailor your test prep strategy to the style of the test. This section will address the foundation of your math preparation, so don’t skip it and be sure to read it carefully!
The Math portion of the SAT comprises of two sections that are the third and fourth sections in the overall test. The first Math section (“no-calculator section”) is 25 minutes and does not allow students to use a calculator to answer its 20 questions. 15 of the questions are multiple choice, while 5 of them are grid-in. The second section (“calculator section”) is longer and a bit more complex – students have 55 minutes to answer 38 questions, but are allowed to use a calculator. There are 30 multiple choice questions and 8 grid-in questions.
Thus, when taking the test, students have an average of 1 minute and 15 seconds per question in the no-calculator section and 1 minute and 26 seconds per question in the calculator section. Keep this in mind when taking the test as it’s often the time pressure that can mess up students. One important thing to note about the Math sections are that the questions are not ordered randomly! They are actually ordered from least difficult to the most difficult. This comes into play when figuring out how to allocate your time in different questions.
| No-Calculator Math Section | Calculator Math Section |
| 25 minutes | 55 minutes |
| 20 questions: 15 multiple choice, 5 grid-in | 38 questions: 30 multiple choice, 8 grid-in |
| Average 1 min and 15 sec per question | Average 1 min and 26 sec per question |
| Not allowed to use a calculator | Allowed to use a calculator* |
*Make sure your calculator is one of the approved types you can use during the SAT using this guide! Bringing the wrong calculator is one of the most common errors students unintentionally make, and can lead their test scores to be invalidated. Don’t let this be you!
Each section is scored out of 400 points by converting your raw score (how many questions you got right) to a 400 point-scale. The conversion is not the same each time, however, and depends on the test you take. Each section score is summed to give you your total math score. That means that the maximum score you can get on the math portion of the SAT is 800. The median Math total score (the 50th percentile score) usually hovers between 520 and 530.
Topics Tested
There are four official content areas that are tested throughout both sections of the SAT Math portion. In order to ace the Math sections, you will have to understand the concepts tested in each and be comfortable applying your understanding to actual math problems.
The four official content areas are: Heart of Algebra, Problem Solving and Data Analysis, Passport to Advanced Math, and Additional Topics in Math.
All of the sample questions are taken from the 2023 March SAT.
Heart of Algebra
Topics: linear equations, inequalities, functions, and graphs
Example tasks: graphing a linear equation, determining how a graph transforms based on a change in the equation, simplifying an expression, interpreting a linear function
Sample Question

This question is asking you to solve a system of linear equations. You are given two equations that each have the variables x and y. You can use both equations to figure out the “solution” or values that x and y take on. Try to figure out this question yourself, and check your answer using this step by step breakdown on how to approach this problem.
Solution
The easiest method to solve this problem is to solve for one variable (x or y), then plug in the expression you get into the other equation. This allows you to manipulate the two equations so that you are only solving for one variable at a time.
- This question is pretty nice because it already gives you both equations in “y =” form. Usually, you would have to isolate the variable yourself.
- Lets use the bottom equation to plug into the top one. Since they give you that y = -14x – 7, you can plug the entire right-hand expression into the y-variable on the top equation.
- The top equation will now look like this: -14x – 7 = 18x + 25
- This is now a simple algebra equation where you can solve for x.
- Doing the algebra, you discover that x = -1.
- Then, you can plug in x = -1 into either the top or bottom equation to find y.
- Doing the algebra, you discover that y = 7.
- Your final answer will be B, (-1, 7).
Note that you can also do this in the opposite way – solving for x first, then using it to find y. It is just more complicated to do this in this case because y is already solved for you in the given question.
Problem Solving and Data Analysis
Topics: ratios, percentages, and interpreting data from charts, graphs, and tables.
Example tasks: using tables to analyze data and trends, using info from a chart to determine exponential growth (ie. population sizes), using scatterplots to calculate the mean, mode, or range of a data collection.
Sample Question
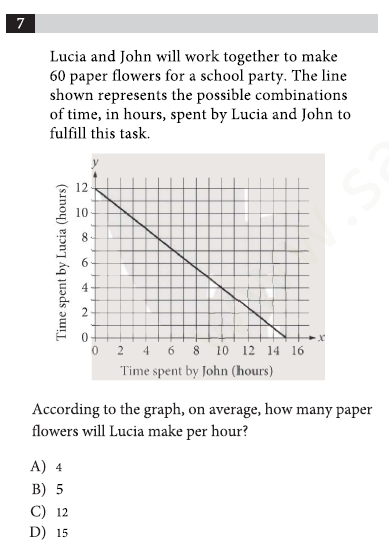
This question is asking you to interpret data from a graph. You are given a linear graph, and a short blurb with context on what the graph represents. Try to figure out this question yourself, and check your answer using this step by step breakdown on how to approach this problem.
Solution
When interpreting data from graphs, it’s important to pay special attention to the axis labels. This helps you understand what the graph is modeling, how it relates to the blurb, and what they’re asking you to find.
- First, lets read the context. The blurb tells us that Lucia and John are making a total of 60 paper flowers for a school party. 60 is an essential number to remember here. The blurb even tells you what the graph is modeling – no need to interpret it for yourself. It models possible combinations of how much time Lucia and John can each put in to making the 60 flowers.
- Reading the graph, we can see that to make 60 flowers, the following combinations are possible:
- Lucia can spend 12 hours, while John spends 0 hours (John isn’t being super helpful here!)
- Lucia can spend 9 hours, while John spends 4 hours
- Lucia can spend 3 hours, while John spends 11 hours
- Lucia can spend 0 hours, while John spends 15 hours (Lucia isn’t being super helpful here!)
- You can get the interpretations above by picking a point in the line and tracing left for Lucia’s hours and tracing down for John’s hours.
- The question is asking you to focus on Lucia: How many paper flowers will Lucia make per hour, on average?
- To answer this you must find find how long it takes Lucia to make 60 flowers without John’s help (when his hours = 0). From the graph, Lucia takes 12 hours to make all the flowers by herself. That’s about 5 flowers per hour (60 flowers divided by 12 hours = 5).
- You want to look at this particular data point because the question is just asking what Lucia can do by herself, not with John’s help. All the data points take into account John helping out in one way or another.
- Your final answer is B, 5.
Passport to Advanced Math
Topics: nonlinear equations.
Example tasks: solving quadratic equations, determining the curve of a graph, dividing polynomial expressions, using rational exponents to solve equations.
Sample Question
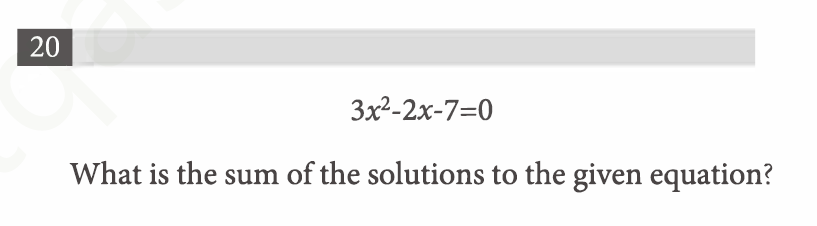
This question gives you a quadratic equation and asks you to add all the possible solutions to the equation. You know it is a quadratic because it is a second-degree algebraic expression, in other words, it takes the form of: ax^2 + bx + c = 0, where a, b, and c are known numbers and x are the unknowns. The solutions to the quadratic are the values of x. Try to figure out this question yourself, and check your answer using this step by step breakdown on how to approach this problem.
Solution
When you are asked to find the solutions to a quadratic equation, your instinct should be to either factor it (if possible) or to use the handy quadratic formula. Some quadratic equations are easier to factor than others – usually, those with a = 1 are easy to do in your head. In this case, however, a = 3, so we are better off just plugging it into the quadratic formula.
- The quadratic formula is:
- If you don’t have it memorized, memorize it ASAP! This is one of the most important formulas to know, not just for the SAT, but for high school and college math in general. If you’re having trouble memorizing it, there are a bunch of catchy songs on YouTube that will have it stuck in your head in no time.
- Now that you have the formula, plug in the quadratic equation that was given to you!
- Having trouble figuring out what a, b, and c are? We know that a quadratic equation has the form ax^2 + bx + c = 0. In this case, the equation given to us is already set to 0, so the integers automatically correspond to a, b, and c depending on which x accompanies it!
- So, from 3x^2 – 2x – 7 = 0, we can extract that a = 3, b = -2, and c = -7. Don’t forget the negative signs for b and c.
- Plugging this into the formula, you get:
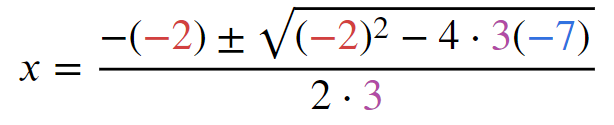
- After doing out all the math:
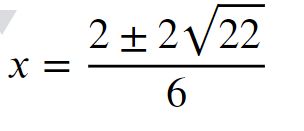
- Don’t forget that the plus/minus sign means that there’s two separate solutions – one positive, and one negative!
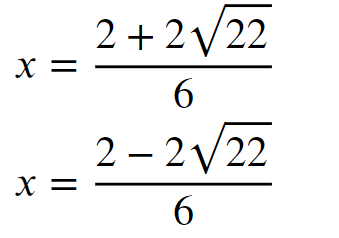
- Because they are the same values, just one positive and negative, if you sum the two together, you will get zero. They cancel each other out.
- Your final answer is 0.
Additional Topics in Math
Topics: geometry, trigonometry, and complex numbers
Example tasks: determining the area or volume of a shape, calculating arc length, using sine, cosine, and tangent to solve word problems.
Note that topics from this section make up only about 10% across the two SAT Math sections. But, it is still important for you to study these topics, especially if you’re aiming for a top or perfect score!
Sample Question

This is a geometry question that is asking you to find the volume of the drawn shape – a cone and a hemisphere connected at the base. While this question might look complex and daunting, it is a simple volume question when you break it down into pieces. A hemisphere is just half of a sphere, so you will need to know the formulas for the volume of a sphere and a cone. Lucky for you, these formulas are actually given to you by the SAT in the formula sheet at the beginning of the section! Remember which formulas are given to you, so that you can refer back to them when needed. Try to figure out this question yourself, and check your answer using this step by step breakdown on how to approach this problem.
Solution
- The formulas of a sphere and a cone are as follows:
- The question should give you all the information you need to find the volume. This means that, in the information provided, you can find the radius of the sphere and the radius and height of the cone.
- To find the radius of the sphere: The answer gives you the diameter of the base of the hemisphere, which is 6 cm. This means that the radius is half of that, 3 cm.
- Therefore, you can find the volume of the hemisphere by finding the volume of a sphere with a radius of 3 cm, then divide it in half.
- Volume of sphere with radius of 3cm: (4/3) * π * 3^3 = 36π
- Volume of hemisphere = 36π / 2 = 18π
- To find the radius and height of the cone: The radius is the same as the hemisphere, which is 3 cm. The height is the total height given (9 cm), minus the height of the hemisphere. You know that the radius is 3 cm, which is the length from the center of the hemisphere to any point at the edge. This includes the length perpendicular to the base, in other words, the length from the base to the top. That means that the radius is also the height of the hemisphere. Therefore, the height of the cone is 9 cm – 3 cm, which is 6 cm.
- Therefore, you can find the volume of the cone by plugging this information into the formula:
- Volume of cone with radius of 3 cm and height of 6 cm: (⅓) * π * 3^2 * 6 = 18π
- You now have the volume of the hemisphere and the volume of the cone. Adding them together, you get the total volume of the figure: 18π + 18π = 36π.
- Your final answer is B, 36π.
Digital SAT: Math
The SAT will be transitioning to its digital version in 2024, and it’s important to keep several things in mind as to how the Math section will change or stay the same.
Check out this article to see what topics are covered on the Digital SAT Math section. Because of the switch to digital format, you should also familiarize yourself with the new tools that are built-in to the Digital SAT, including the calculator for Math sections.
How To Study For SAT Math
Now that you are familiar with the structure, format, and types of questions that will be asked on the SAT Math sections, you can start your preparation journey to acing them. How should you study for SAT Math? Sometimes the hardest part is just figuring out where to start. While students will need to practice different topics and aspects of the test (ie. time management), there are a few basic steps everyone can take to approaching their SAT study journey.
While all students can follow this general study plan, one way to take your studying to the next level is to hire a tutor. Tutors, like ones at SoFlo, will draw on past experiences and time-tested strategies to identify your strengths and weaknesses and create a tailored study plan for you. This study plan will include the elements listed below, but will probably be more relevant to your skills and situation. Of course, it isn’t necessary to hire a tutor to do well, but many students benefit from the accountability a tutor will demand from you and a tailored curriculum with extra guidance and help.
1. Become Acquainted With The SAT Math Content
As I mentioned earlier, this should be everyone’s first step in preparing for the SAT Math section! Luckily, you will have studied and read the previous section carefully, which outlined all the fundamentals you need to know. Once you feel comfortable with this information, move on to the next steps.
2. Assess Your Weaknesses And Strengths
This is a crucial step that will give your study plan direction and efficiency. Approaching the SAT with the mindset that you have to study everything in an equal manner is an inefficient allocation of your time and effort. You may have algebra on lock and only need a few problems a week to brush up, while geometry may need significantly more time and effort to memorize all the formulas and practice those types of problems. It all depends from person to person. Reflect on your skills and experiences at school: Were there certain topics that gave you grief? Do you still remember how to do math problems from middle school? Are there certain topics that you haven’t covered yet in the classroom that are covered on the SAT?
Take stock of what you know about yourself, and you can forge ahead with more clarity.

3. TAKE A PRACTICE TEST
Reflection is important, but can only go so far. Taking the practice test is one of the most definite ways to pinpoint your strengths and weaknesses, specifically on the SAT. There are numerous free SAT practice tests online that you can find – here at SoFlo, we have a whole vault of official practice tests dating back to 2016. It is important that you take the practice test under the time limit so you can see how it feels to solve problems under pressure, and if that becomes an issue you need to work on.
After taking the practice test, go through the questions you got wrong and categorize them into topics (ie. Geometry, Algebra, Exponents, Data Interpretation, Probability, etc.). Also, take special note of questions that you had no idea what to do, or forgot a key piece of information. These are topics you need to especially focus on and important formulas that you need to memorize.
4. Aim For A Specific Score
Based on the results of your practice test and the list of colleges you are planning to apply to, set a target score. Don’t know how to set a target score? Here is a guide to help you do so. In short, it should take into account what is feasible for you to accomplish and what you need to be a competitive applicant to the colleges you are applying to.
5. Create A Study Plan
Based on your reflection and the results of your practice test, you can create your own study plan. Plan it out week-by-week, and, if you need it, day-by-day. Figure out what topics you will cover, how many problems you will solve, and how many practice tests you will take (take at least one a week). The frequency and quantity of practice depends on your schedule and how close the test date is.
Students underestimate the negative effects of cramming. Cramming is not only severely stressful and negatively impacts your test performance because of lack of sleep, but it will also almost never lead to your best results. The SAT is a long test that covers many complicated topics. You need time to really understand all of these problems and practice enough to feel confident and comfortable on test day. Even if you are a great student in school, taking the SAT with little or no preparation can backfire since the testing style and format can be extremely different to what you know from school.
Save yourself the stress (and the money!) by planning ahead and starting to prepare for the SAT at least 3 months before your testing date. You and your score results will thank your past self immensely.

6. Memorize Core Formulas
One integral part of your study plan should be to memorize core math formulas. The SAT provides some formulas, but not all, that are essential to answering all the questions in the section. There are numerous articles online that list the math formulas you should know, but it is a good practice to also build one of your own. When you are doing practice problems or practice tests, and you stumble across a question using a formula you haven’t memorized, note it down. Add it to your existing “to-memorize” list, and don’t forget it the next time!
Memorizing formulas is also important for speedy test taking. Having a formula ready at the tips of your fingers removes time trying to remember it. Every second counts on the SAT!
7. Put TACTics Into Use
There are smarter ways to solve problems on the SAT Math, and you should take advantage of them in order to do your best. Strategies like answer elimination and numerical shortcuts can help save time and improve accuracy. You can find numerous strategies online, but here are 12 SAT Math Tips And Tricks that SoFlo tutors has specifically picked out for students.
8. Improve Your Speed
Lastly, time management is one of the biggest skills that students have to work on when preparing for the SAT Math sections. It is a whole different beast to be completing math problems under timed pressure, compared to when you’re just solving math problems for homework. One way to improve your speed is to always solve practice problems under a timer. Remember that on the no-calculator section, you have an average of 1 minute and 15 seconds to solve each problem and, in the calculator section, you have an average of 1 minute and 26 seconds. Set these time limits at first. Once you’re beating it, lower your time limit. The faster you can do problems, while maintaining your accuracy, the better, especially because you will want time at the end to check your work and even more extra time to think through those tricky problems at the end.

What It Takes To Get An 800 In Math
Taking the steps to understand the SAT Math Section and creating a study plan is essential to reaching your target score. Many students gunning for top schools, however, like Harvard and MIT, might set themselves a high goal of achieving an 800 – a perfect total score. Please note that by no means do you have to achieve this perfect score to gain admission into schools like Harvard and MIT. These schools practice holistic admissions, which takes into account all aspects of your application, like your grades, extracurriculars, essays, and recommendations. The testing standards of these schools are definitely high, but they don’t expect you to be perfect all the time.
If you’re still bent on receiving that perfect 800 score, however, you will need to think about what is feasible for you to do to get there. This differs between people. Usually, people who excel in math aim for this score, so the preparation isn’t as arduous as for someone who considers themselves weak in the subject. Undeniably, however, unless you are a math genius, you need to have some degree of preparation to ace the SAT Math section. This means preparing well ahead of time and making sure you know every single topic like the back of your hand.
SoFlo Tutors: Your Best Way To Study For SAT Math
Looking on the best way to prepare for the SAT Math section? Aiming for that perfect 800 score? Check out SoFlo SAT tutoring for expert help on the SAT Math section. All of our tutors attend top universities around the nation and scored in the 99th percentile on their SAT. They will work one-on-one on you to identify and improve your weak areas and increase your chances of getting your target score. Our tutors schedule to sessions to your availability and our costs start at $60/hour. Check out our tutoring services to book a session!
About The Author
Andie Pinga is an expert SoFlo tutor and graduated from the University of Pennsylvania with a B.A. in Economics and a minor in Anthropology. She scored a 35 on her ACT and enjoys rock climbing and playing the guitar.










